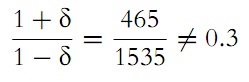
Main article.
As we can see, the probability of a letter being a vowel changes considerably depending upon which letter - vowel or consonant - precedes it. The difference p1 - p0 , which we denote with the [Greek] letter δ is
Now, if we assume that the sequence of 20,000 letters forms a simple chain, then for
according to "Investigation of a Remarkable Case of Dependent Samples" the number
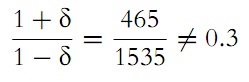
can be regarded as the theoretical dispersion coefficient; naturally, this number does not agree exactly with the previously found
but it is closer to it than to one, which corresponds to the case of independent samples.
If we consider the sequence as a complex chain and apply the findings of the study
"On a Case of Samples Connected in Complex Chain" we can make the theoretical
dispersion coefficient agree still better with the experimental one.
For this, we count the number of the combinations
and
in our sequence.