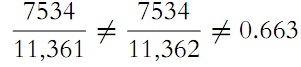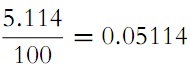
Main article.
Now, if we move on from samples in hundreds to single samples, we ascertain that the number
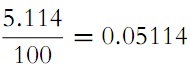
differs strongly from
the coefficient of dispersion (we deviate here slightly from usual terminology, whereby we should have taken the square root of the number that we call the coefficient of dispersion) is
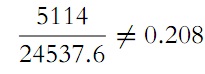
that is, approximately 1/5 , which is explained well by the connectedness of our samples.
To clarify this connectedness, although not entirely, it will help us to calculate the
above-mentioned probabilities p1 and p0 approximately.
We take the entire text of 20,000 letters, count the number of sequences
and obtain the number 1104; after dividing it by the total number of vowels in the text, we get the following approximate quantity for p1:
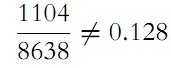
In the same manner, we could find an approximate value for q0 by counting the number of sequences
and dividing it by 11,362, then p0 = 1 - q0 . However, we can also substitute the tiring direct count with the following. If we subtract 1104 from 8638, we obtain the number of consonants
which follow a vowel, and as all consonants apart from the first one must follow either a vowel or a consonant, the number of sequences
is determined by the difference