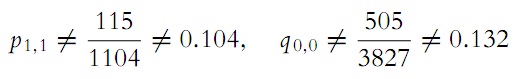
Main article.
According to my count, there are 115 cases of the first combination and of the second - 505. When we divide these numbers by the numbers found earlier
we get the approximate equations
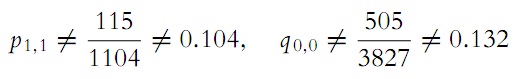
With the aim of applying the findings of the above-mentioned article to our case here, we assume that
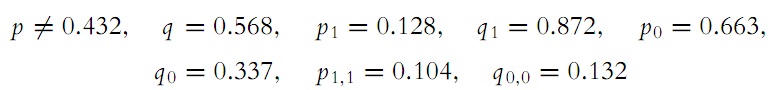
and from these numbers we get
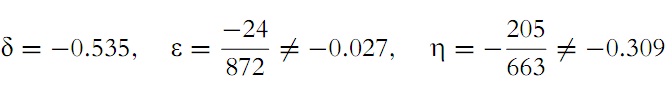
Next, we turn to the expression of the coefficient of dispersion
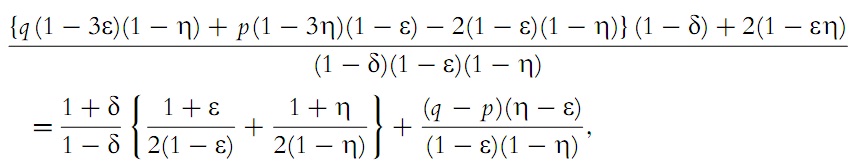
which corresponds to the conditions of my article and is derived there.
If we insert here the values found
and calculate the result, we obtain
as coefficient of dispersion, which agrees very well with the number
found following general rules and independent of our special assumptions, so that one can hardly demand any better agreement.