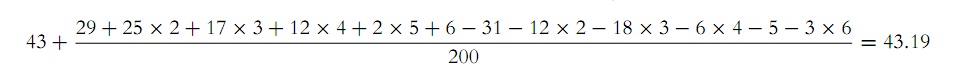
Main article.
With the aid of this table, the arithmetic mean is easy to find:
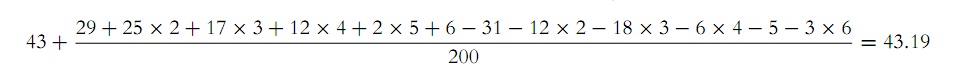
and from this it follows that
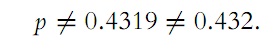
Next, we calculate the sum of the squares of their deviations from 43.2; it is 1022.8, divided by 200, we get 5.114,and this number can be regarded as the approximate quantity of the mathematicalexpectation of the square of the deviation of each of our 200 numbers from theircommon mathematical expectation, which is 43.2. Finally, the number:

represents the approximate quantity of the mathematical expectation of the square of the error when determining 100 p with the equation
Such a deduction is associated with the usual assumption of the method of least squares, namely, that we are dealing with independent quantities. This assumption is not less justified in this case than in many others, because the connection between the numbers is fairly weak due to the way in which they were obtained. One can also discern a certain correspondence of our results with the well-known law of error, which is associated with the names of Gauss and Laplace; for example, the quantity called probable error in our case is
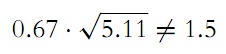
and accordingly, between
lie 103 numbers, that is, approximately half [of the total]: 31 times the number 42, 43
times the number 43, and 29 times the number 44.
To the independence of the quantities corresponds the fact that when we combine
them in twos, fours, or fives, and calculate for these 100, 50, and 40 combinations the
sums of the squares of their deviations from
we obtain the numbers
which do not differ very much from the number found earlier