3. Язык Пролог в задачах и примрах

3.1. Программирование с помощью фактов и правил
3.1.2. Первая формулировка задачи поиска в пространстве состояний 51 ад
3.1.3. Реализация на Прологе простой вопросно-ответной системы
3.2. Рекурсии
Упражнения
3.3. Программирование циклических процессов.
3.4. Работа со списками
3.4.1. Описание списков в программе
3.4.2. Добавление элемента в список
3.4.3. Удаление элемента
3.4.4. Принадлежность элемента списку
3.4.5. Сцепление (конкатенация) списков
3.4.6. Удаление из списка повторяющихся элементов
3.4.7. Вычисление суммы элементов списка
3.4.8. Обращение списка
3.4.9. Нахождение максимального элемента списка
3.4.10. Перестановки
3.4.11. Примеры использования списков
Упражнения
3.5. Виды рекурсии
3.6. Поиск в пространстве состояний
Упражнения
3.6.0 Использование структур
3.6.1. Объявление структур
3.6.1. База данных с использованием структур.
3.6.2. Задача «Ханойская башня».
3.6.3. Задача о перевозке через реку волка, козы и капусты
3.6.4. Планирование воздушного путешествия
3.6.5. Реализация Планировщика в терминах структур
3.6.6. Задача «Зебра»
Упражнения
3.7. Динамическая база данных
3.7.1. Использование стандартных предикатов динамической базы данных
Упражнения
3.8. Средства управления
3.9. Представление множеств двоичными деревьями
3.9. Программы классификации
3.9.1. Программа классификации с обратной цепочкой рассуждений
3.9.2. Программы классификации с прямой цепочкой рассуждений.
3.9. Обработка текстов
Упражнения
3.10. Примеры

3.1. Программирование с помощью фактов и правил

Рассмотрим следующую вводную Пролог-программу. На этом примере мы покажем, как создать, отредактировать и выполнить Пролог-программу в интегрированной среде PDC Prolog.

predicates
hello
clauses
hello :-
makewindow(1,7,7,"My first program",4,36,10,22),  % Создание окна
nl,                                                                                        % Перевод строки     
write("  Please type your name "),                                      % Вывод текстовой строки
cursor(4, 5),                                                                         % Позиционирование курсора
readnl( Name ),                                                                   % Ввод строки в переменную Name
nl,
write("  Wellcome  ", Name).                                              % Вывод текстовой строки и переменной
goal
hello.

После исправления ошибок в программе выберите опцию RUN в меню PDC Prolog. Введите свое имя (например, Аня) в окне ввода и нажмите ENTER. Программа напечатает
Welcome  Аня
и будет ждать нажатия клавиши пробела (SPACE BAR).
Работа программы всегда начинается с выполнения раздела Goal. Цель пытается удовлетворить предикат  hello. Этот предикат не имеет аргументов, его описание есть в разделе Predicates. Имеется единственная статья Clauses для этого предиката. Поэтому для проверки истинности цели начинают последовательно выполняться предикаты, записанные в правой части предиката hello. Все эти предикаты являются встроенными (стандартными), поэтому в программе не требуется их описания.
Эту небольшую программу привели только для демонстрации запуска полностью готовой программы в среде PDC Prolog. Она похожа на процедурный стиль программирования и напоминает, скажем так, реализацию некоторой логической функции (поскольку предикат, как логическая функция, может принимать только одно из двух значений – истина или ложь). Данный пример приведен, чтобы искушенный в программировании пользователь смог провести аналогию между процедурным стилем программирования и возможностью его реализации на Прологе.
Второй пример сделаем уже в прологовском стиле. Пролог – это язык программирования, предназначенный для представления и использования знаний о некоторой предметной области. Более точно, предметная область – это множество объектов вместе со знанием о них, выраженном в виде отношений. Эти отношения описывают свойства объектов и связи между ними. Описания представлены в виде фактов и правил. Это описание статическое, само по себе оно никакого процесса вычисления не задает. Чтобы программа заработала, необходимо указать цель.
Оформим факты и правила примера из раздела 1.2 в виде работающей Пролог-программы, добавив секцию описания предикатов Predicates и название секции их реализации Clauses:
Predicates
likes( string, string )
clever ( string )
Clauses
likes( ellen, reading ).
likes( john, football ).
likes( tom, baseball ).
likes( eric, reading ).
likes( mark, tennis ).
clever ( X ) :- likes ( X, reading ).
Эта программа может выполняться в интерактивном режиме (режиме диалога), поскольку цель явно не записана в программе (отсутствует секция Goal).
Запустите среду PDC PROLOG и наберите в окне редактора текст этой программы. После исправления синтаксических ошибок в программе в процессе компиляции выберите опцию RUN в меню Пролога. В этой программе цель не указана (которая, вообще говоря,  в отладочном режиме не обязательна), поэтому, когда система в отдельном диалоговом окне после приглашения «Goal:» запросит цель, сразу после двоеточия введите запрос:
Goal: likes( john, football ).
Пролог ответит
Yes ,
поскольку такой факт имеется. Каким образом отыскивается этот факт в базе данных – это уже забота самой Пролог-системы. Программист только сообщает системе то, что ему известно и задает вопросы.
Заметим, что хотя программа и в таком виде будет работать, более грамотным является запись программы с указанием областей определения переменных:
domains
name, hobby = string
Predicates
likes( name, hobby )
clever ( name )
Clauses
likes( ellen, tennis ).
likes( john, football ).
likes( tom, baseball ).
likes( eric, swimming ).
likes( mark, tennis ).
clever ( X ) :- likes ( X, reading ).
2. Построение  базы данных. На Прологе чрезвычайно просто организовать реляционную базу данных в виде набора некоторых фактов и реализовать всевозможные запросы в виде правил. Пусть база данных содержит следующие сведения об автомобилях: марка машины, год выпуска, цвет, цена:
Predicates
car( string, integer, string, integer )
Clauses
car( volvo, 1990, red, 1800 ).
car( toyota, 1988, black, 2000 ).
car( ford, 1994, white,    3000 ).
Наберите эту программу согласно правилам оформления Пролог-программы и исполните команду RUN. Когда система запросит цель, введите запрос:
Goal:  car( toyota, _ , _ , _ ).
Пролог ответит
1 solution
Yes
в диалоговом окне и будет ждать, когда вы введете другую цель.
В этом запросе использовались анонимные переменные, обозначенные символом подчеркивания. Анонимная переменная используется для обозначения аргументов, значения которых в данный момент могут быть произвольны. Если анонимная переменная встречается в запросе, то ее значение не выводится при ответе системы на этот запрос. Анонимная переменная может также использоваться в записи предикатов, если в предложении она встречается один раз. Примеры записи таких предикатов встретим дальше.
Если зададите в качестве цели
Goal:  car( mersedes, 1990, _ , _ ) ,
система ответит
No solution,
поскольку наша база данных не содержит такого утверждения.
Теперь предположим, что мы хотим узнать все марки машин, имеющиеся в базе данных, т.е. задать вопрос: "Каковы те объекты Х, которые являются марками машины?". Тогда наш вопрос запишется так:
Goal:  car( X, _ , _ , _ ).
Пролог ответит:
X = “volvo”
X = "toyota"
X = "ford"
3 solutions.
Можно также задавать вопросы более общего характера. К примеру, если требуется найти все машины, выпущенные до 1992 года, то следует задать запрос, который представляет конъюнкцию целей:
Goal  car( X, Y, _ , _ ),  Y < 1992.
X = “volvo” Y = 1990
X = "toyota" Y = 1988
2 solutions.
Подобная база данных имеет вид целостных информационных объектов. Более гибким является представление базы данных в виде бинарных отношений, в которых один из атрибутов должен выступать в роли ключа, объединяющего все остальные свойства. Пусть в нашем примере это будет марка машины:
year( volvo, 1990 ).
year( toyota, 1988 ).
year( ford, 1994 ).
color( volvo, red ).
color( toyota, black ).
color( ford, white ).
cost( volvo, 2000 ).
cost( toyota, 2500 ).
cosr( ford, 3000 ).
В случае необходимости атрибуты можно собрать в единое целое с использованием переменных при помощи правила:
car( M, Y, C, P ) :–  year( M, Y ), color( M, C ), cost( M, P ).
Правило в данном случае является обобщением всех фактов.
Определим теперь запрос, выполняющий поиск старых автомобилей, в виде правила «старый автомобиль»:
old_car( M, Y ) :- car( M , Y, _ , _ ),  Y < 1992.
Это правило добавим к основной программе, не забыв включить го описание в раздел Predicates, а обращаться к нему можно, задав цель:
 Goal:  old_car( X, Y ).
Даже уже в этой простой программе мы вплотную подошли к одному из определений базы знаний. База знаний – это набор фактов и правил. Пока у нас было описание машин в виде фактов, это была база данных. Как только программу дополнили правилами, т.е. указали способ использования данных, мы перешли уже к базе знаний.
4. Любитель проводить аналогию между различными языками программирования уже догадался, что Пролог-программа ведет себя так, как если бы каждая строка программы начиналась с ключевого слова IF (ЕСЛИ). Поэтому разветвляющиеся алгоритмы реализуются в Прологе достаточно прямолинейно.
Программа решение квадратного уравнения – типичный пример реализации на Прологе разветвляющегося алгоритма. В комментариях приведена интерпретация предикатов.
predicates
solve( 0real, real, real ) % Запуск программы
reply( real, real, real )               % Ветви вычислений
clauses
solve( A, B, C ) :–
D = B * B – 4 * A * C, % Вычисление дискриминанта
reply( A, B, D ), nl.                % Здесь запускаются разветвления вычислительного процесса
reply( _ ,  _ , D) :– D < 0,
write( "No solution" ).
reply( A, B, D ) :– D = 0,
X = - B / ( 2 * A ), write( "x1,2=", X ).
reply( A, B, D ) :– D > 0,
SqrtD = sqrt( D ),
X1 = ( - B + SqrtD) / ( 2 * A ),
X2 = ( - B – SqrtD) / ( 2 * A ),
write( "x1 = ", X1," and x2 = ", X2 ).
Goal  solve( 3, 4, 5 ).
На этом примере видно, что главный способ реализации разветвлений в Пролог-программе – обращение к некоторому предикату, который реализуется с проверкой заданных условий (в нашем случае – предикат reply).
В этом примере также видим использование анонимной переменой в первом предложении предиката reply:
reply( _ ,  _ , D) :– D < 0, write( "No solution" ).
Оно говорит, что если дискриминант D меньше нуля, неважно, какие значения имеют коэффициенты A и B.
Рассмотрим другой пример в качестве упражнения по автоматизации логического вывода. Имеется следующая задача из психологического практикума.
Бутси – коричневая кошка. Корни – черная кошка. Мак – рыжая кошка. Флэш, Ровер, Спот – собаки, Ровер – рыжая, а Спот – белая. Все животные, которыми владеют Том и Кейт, имеют родословные. Том владеет всеми черными и коричневыми животными, а Кейт владеет всеми собаками небелого цвета, которые не являются собственностью Тома. Алан владеет Мак, если Кейт не владеет Бутси и если Спот не имеет родословной. Флэш – пятнистая собака. Определить, какие животные не имеют хозяев. (Ответ: Спот).
Для интерпретации формул исчисления предикатов требуется задать области интерпретации предметных переменных, что делается в разделе Domains
Domains
animal_name, color, name = string
Описание предикатов включает имена предикатов и перечисление имен предметных переменных:
Predicates
cat( animal_name )
dog( animal_name )
color( animal_name, color )
have( name, animal_name )
rodosloмnaya(animal_name )
animal( animal_name)
Факты и правила следующие:
Clauses
/* Факты, перечисляющие клички и расцветки животных */
cat( butsi ).         cat( korni ).      cat( mac ).
dog( rover ).       dog( fles ).       dog( spot ).
color( butsi, brown ).
color( korni, black ).
color( mac, yellow ).
color( rover, yellow ).
color( spot, white ).
color( fles, black_and_white ).
/* Животное – это кошка или собака*/
animal( X ) :– cat( X ); dog( X ).
/* Животные, имеющие родословные */
rodoslovnaya( X ) :– animal( X ), have( tom, X ).
rodoslovnaya( X ) :– animal( X ), have( keit, X ).
/* Том владеет всеми черными или коричневыми животными */
have( tom, X ) :– color( X, black ); color( X, brown ).
/* Кейт владеет собаками */
have( keit, X ):–dog( X ),
not( color( X, white )),
not( have( tom, X )).
/* Алан владеет Мак */
have( alan, mac ) :– not( have( keit, butsi )),
not( rodoslovnaya( spot )).
/* Цель – найти животное Х, не имеющее владельца */
goal
animal( X ), not( have( _ , X )),write( X ).
Цель организует запрос к программе и выводит результат. Процесс доказательства включает в себя как поиск нужных подстановок, которые делают истинными утверждения, так и выполнение встроенных предикатов. Например, not – встроенный предикат отрицания, write( ) – вывод значения переменной.  
Каждое предложение раздела Clauses представляет собой формулу вида:
D <– A & B & … & C.
Например, предложение
 rodoslovnaya(X):–animal(X), have(tom,X).
представляет собой формулу
animal(X) & have(tom,X) –> rodoslovnaya(X),

причем порядок следования элементов конъюнкции определяет последовательность процесса доказательства по методу резолюций и может имеет важное значение.

3.1.2. Первая формулировка задачи поиска в пространстве состояний 51 ад

Простые факты иллюстрируют возможность моделирования системы, находящейся на каждом шаге в некотором состоянии, из которого она может перейти по одному из правил перехода в следующее состояние. Этот процесс недетерминированный, поскольку система может перейти не в одно состояние.
В качестве примера рассмотрим классическую задачу поиска пути в пространстве состояний . Это задача о перевозке через реку волка, козы и капусты.
Формулировка задачи.
Крестьянин должен перевезти в лодке через реку волка, козу и капусту. Вместе с человеком в лодке может поместиться или волк, или коза, или капуста, причем человеку приходится охранять козу от волка и капусту от козы.
Такая задача описывается пространством состояний. Пространство состояний - это граф, вершины которого соответствуют ситуациям, встречающимся в задаче, а решение задачи сводится к поиску пути в этом графе между заданной начальной ситуацией (стартовой вершиной) и некоторой конечной ситуацией, называемой целевой вершиной.
Для определенности рассмотрим ситуацию остающихся каждый раз на одном берегу реки. Рассмотрим общую схему вывода. Ради краткости нотации примем следующие обозначения констант: f – крестьянин, w – волк, g – коза, c – капуста.
move( f, w, g, c ) :- move(w, c ).            % Крестьянин уплыл вместе с козой
move( w, c ) :- move( f, w, c ).  % Крестьянин вернулся один
move( f, w, c ) :- move( c ).                   % Крестьянин уплыл с волком
move( f, w, c ) :- move( w ).                  % или уплыл вместе с капустой
move( c ) :- move( f, g, c ).                    % Крестьянин вернулся обратно вместе с козой
move( w ) :- move( f, g, w ).                  % Крестьянин вернулся обратно вместе с козой
move( f, g, c ) :- move( g ).                   % Коза осталась одна
move( f, g, w )  :- move( g ).
move( g ) :- move( f, g ).                        % Крестьянин вернулся за козой
move( f, g ) :- move( ).                           % Никого не осталось
move( ).                                                % Останов
Для придания программе вид рабочей требуется каждое правило дополнить оператором вывода текущего состояния, т.е. текста, который у нас пока что заключен в комментарий. Например, первое правило будет выглядеть так:
move( f, w, g, c ) :- move(w, c ), write(“Фермер уплыл вместе с козой”), nl.
Отметим, что рабочий предикат move следует определить несколько раз на различном количестве аргументов. В Прологе такой синтаксис вполне допустим:
Predicates
move( string, string, string, string )
move( string, string, string )
move( string, string )
move( string )
move
В качестве цели для запуска процесса вывода укажем начальное состояние:
Goal move( f, w, g, c ).
Эта задача имеет не единственное решение, а именно, два. Можно найти их все, если воспользоваться приемом возврата к поиску других решений (включить бэктрекинг).

3.1.3. Реализация на Прологе простой вопросно-ответной системы

Наша цель – написать программу, способную делать рассуждения. Эта программа в какой-то степени будет приближением к экспертной системе. Существует две основных стратегии рассуждений: прямые и обратные. Рассмотрим два примера.

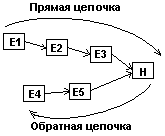
Рис. Прямая и обратная цепочки рассуждений

Прямая цепочка рассуждений: если условие E1 верно, то переход к Е2,  если E2 верно, то переход к Е3 и т.д. до Н, т.е. все отношения Е1, Е2, … должны быть истинны. Рассуждения начинаем с Е1 и система делает суждение об истинности1 Н. Если эта цепочка неверна, начинаются рассуждения от Е4. Прямые рассуждения всегда идут от данных (известных фактов), на каждом шаге вывода применяются все допустимые (с истинными посылками) правила, которые порождают новые факты, до тех пор пока не будет порожден факт-цель.  
При обратной цепочке рассуждений система сначала рассматривает суждение Н. Оглядываясь назад, она выясняет, что для установления истинности Ней надо знать Е3, а чтобы знать Е3, ей требуется знать Е2, а чтобы знать Е2, надо знать Е1. Поэтому система запрашивает данные о Е1, Е2, затем Е3 и после этого делает вывод об истинности Н. Обратные рассуждения идут от цели.
Теперь вспомним, какая стратегия применяется в Прологе. Конструкция вида
ЕСЛИ а ТО b
в синтаксисе Пролога выглядит:
b :- a.
То есть логический вывод идет от цели, а это обратная цепочка рассуждений. Таким образом, обратные рассуждения в Прологе могут быть реализованы достаточно прямолинейно.
Подходящей задачей, при решении которой можно использовать обратную цепочку рассуждений, может быть задача, вытекающая из следующей ситуации: к директору некоторой фирмы пришел человек, желающий устроится на работу. Директор располагает сведениями о его квалификации, о потребностях фирмы в специалистах и ему нужно решить, какую должность в фирме может занять посетитель. Поскольку в задаче надо выбрать один из нескольких возможных вариантов (должностей), для ее решения можно воспользоваться обратной цепочкой рассуждений
Система рассуждений директора может быть примерно следующая: 64 Левин
ЕСЛИ у посетителя нет диплома
ТО посетителю отказать в приеме на работу.
ЕСЛИ посетитель имеет диплом
И  он сделал важное открытие
ТО предложить посетителю должность научного сотрудника.
ЕСЛИ средний балл за время учебы >=3.5
ТО предложить посетителю должность инженера-конструктора.
ЕСЛИ средний балл <3.5
И  посетитель работал по специальности >2 лет
ТО предложить посетителю должность инженера по эксплуатации
ЕСЛИ средний балл <3.5 лет  
И  стаж работы <2 лет
ТО посетителю отказать.
Мы видим, что рассуждения – это логические структуры вида:
ЕСЛИ а1 ТО b
ЕСЛИ а2 И  а3 ТО с,
где а1, а2, а3, b, с – строковые константы, представляющие фрагменты рассуждений.
Такие структуры вида «ЕСЛИ … ТО» называются продукциями, а вся система рассуждений носит название «правила продукций».
Продукции в Прологе можно описать разными способами, например, тройкой «объект, атрибут, значение». В нашем случае для реализации цепочек рассуждений достаточно предикатов двух видов: it_is и this. Чтобы выяснить истинность, например, b, надо выяснить истинность а1:
it_is(b):- this(a1).
Для того чтобы выяснить истинность с, надо последовательно выяснить истинность а2 и а3:
it_is(c):- this(a2), this(a3).
Таким образом, приведенные выше рассуждения можем переписать в виде правил:
it_is(“отказать в приеме на работу”):- not(this(“есть диплом”)).
it_is(“должность научного сотрудника”):- this(“есть диплом”),  
this(“сделал важное открытие”).
it_is(“должность инженера-конструктора”):- this(“средний балл за время учебы >=3.5”).
it_is(“должность инженера по эксплуатации”):- this(“средний балл <3.5”),
this(“работал по специальности >2 лет”).
it_is(“отказать в приеме на работу”):- this(“средний балл <3.5 лет”), 
this(”стаж работы <2 лет”).
Осталось добавить механизм, который будет вести диалог. Чтобы выяснить истинность отдельных высказываний для конкретной ситуации, очевидно проще всего спросить об этом. Эту работу выполнит несложное правило:
this( S ) :-  write( S, ”?” ), readchar( Ans ), Ans = ’y’.
Правило выводит на экран текстовую строку, в конце которой будет дописан знак вопроса, и будет ждать ответ. Очевидно, пользователь введет символ ‘y’ или ‘n’. Если введенный символ ‘y’,  предикат this закончится истинно (сработает проверка Ans=’y’), а если ‘n’ – ложно.
Допишем цель:
Goal it_is( X ),
write(“Наша рекомендация – “, X).
Программа начнет работу  выяснения истинности первого правила. Будет задан вопрос о наличии диплома.  Пользователь введет ответ и в зависимости от этого предикат this(“есть диплом”) закончится истинно или ложно. Поскольку  первое правило содержит отрицание, ответ ‘n’ означает, что it_is(“отказать в приеме на работу”) истинно и работа программы на этом завершится. Если же ответ оказался ‘y’, первое правило буде отвергнуто, начнется проверка следующего правила и т.д.
Заметим, что если у директора есть подобная программа, которая содержит формализованные знания эксперта (а директор в данном случае выступает в роли эксперта), то ему в следующие разы не надо будет отвлекаться на встречу с кандидатами, эту работу он может перепоручить служащему по кадрам.
Продукционные системы моделируют прямые рассуждения. Они обеспечивают модель представления человеческого опыта в форме правил и позволяют разрабатывать алгоритмы поиска по образцу – центральный момент основанных на правилах экспертных систем. Задача о перевозке через реку волка, козы и капусты  предыдущего раздела как раз представляла пример прямых подстановок. Каждый раз срабатывало то правило, образец которого распознавался в левой части предиката. Мы видели, что для реализации прямых рассуждений в системе, которую встроен механизм обратного вывода, следует соответствующим образом переформулировать «базу знаний».
Упражнения на простые факты и правила Задача переливания 185 Ад

Кордемский Б.А. Математическая смекалка. М.: «Наука», 1965

3.2. Рекурсии

В Прологе заложено мощное средство, позволяющее определять некоторые отношения, используя эти же отношения, и называемое рекурсией. Без рекурсии невозможно решать задачи сколько-нибудь ощутимой сложности. Рекурсия в Прологе используется для определения как структур данных (списков, деревьев, графов), так и процедур. Сочетание рекурсивных структур данных с рекурсивными же алгоритмами вычислений позволяет компактно и красиво описывать задачу поиска в пространстве состояний. Описание рекурсивных структур увидим позже, сейчас остановимся на рекурсивных правилах. Подробнее, правило является рекурсивным, если оно вызывает само себя в виде подцели, содержащейся в теле по крайней мере одного из ее утверждений. Вспомним принципы программирования рекурсивной процедуры: рекурсия содержит рекурсивный вызов и обязательно проверку условия, обеспечивающего выход из рекурсии. Последовательность рекурсивных вызовов продолжается до тех пор, пока не встретится ограничение вычислений. Эта часть процесса называется прямым прохождением рекурсии, при этом параметры процедуры заносятся в стек. После достижения граничного условия начинается обратное прохождение рекурсии, параметры извлекаются из стека.
Рассмотрим простой 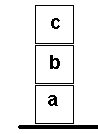пример рекурсивных вычислений. Пусть имеется пирамида, построенная из блоков. Последовательность расположения блоков можно задать предикатом on («на»):
on( c, b ).
on( b, a ).
Определим отношение above («выше»), проверяющее, например, истинно ли то, что блок с выше блока а. Поскольку мы хотим задать универсальное отношение, рассчитанное на пирамиду блоков любой высоты, это отношение будет уже правилом, т.е. содержать переменные. Все отношение можно выразить с помощью двух правил. Первое правило будет верно для блоков, расположенных непосредственно один на другом (отношение on) и его можно сформулировать так:
Для всех X и Y X будет выше Y, если X находится на Y.
Второе правило сложнее, поскольку рассчитано на пирамиду блоков:
Для всех X и YX будет выше Y, если существует такой промежуточный блок Z,
что X находится на Z и Z выше Y.
В синтаксисе Пролога эти два правила определят рекурсивный предикат:
above( X, Y ) :- on( X, Y ).                                  % Нерекурсивное правило
above( X, Y ) :- on( X, Z ), above( Z, Y ). % Правило с рекурсией
Ключевым моментом в данной формулировке было использование самого отношения above в его определении.
Любое рекурсивное определение содержит, по крайней мере, одно нерекурсивное правило и одно или несколько правил с рекурсией. В большинстве случаев имеется по одному правилу каждого типа. Нерекурсивное правило обеспечивает выход из вычислений и таким образом, предотвращает зацикливание. В нашем примере прежде всего проверятся, найдется ли такой блок X, что он расположен непосредственно на Y (нерекурсивное правило). Если найдется, вычисления заканчиваются.
Проследим выполнение рекурсивной процедуры. Соберем все факты и правила вместе и для удобства пронумеруем их. Таким образом, полное пространство поиска следующее:
on( c, b ).                                                     (1)
on( b, a ).                                                     (2)
above( X, Y ) :- on( X, Y ).                             (3)                               
above( X, Y ) :- on( X, Z ),                             (4)
above( Z, Y ).
Goal above( c, a ).
Вычисление начинается от цели above(c, a). Из всех четырех правил этой цели можно сопоставить только правила (3) и (4), из которых подойдет только последнее, поскольку в базе фактов нет факта on(c, a). Используя правило (4), получаем конкретизации переменных X=a, Y=c.  Таким образом, вместо прежней цели возникает конъюнкция новых целей: on(a, Z), above(Z, c). Эти подцели удовлетворяются последовательно. Сначала выполняется первая цель: on(a, Z).Эта цель сопоставляется с одним из фактов, в результате переменная Z унифицируется константой: Z=b. Дальше выполняется вторая подцель above(Z, c), но поскольку к этому моменту переменная Z уже конкретизирована,  цель переписывается:  above(b, c). Опять среди предложений программы (1)-(4) отыскивается подходящее сопоставление, выполняется унификация переменных. Процесс продолжается до сопоставления идентичных фактов. Полное дерево вывода приведено на рис.

Рис. Дерево вывода для цели above(c,a).

Другим примером рекурсивных вычислений является известный алгоритм вычисления факториала. Факториал числа N определяется согласно алгоритму:

1. 1!=1
2. N!=N*(N-1)!

Hа Прологе эта программа может иметь такой вид:
Domains
N, F = real                                 % Вещественный тип имеет больший диапазон
Predicates
factorial( N, F )
Clauses
factorial( 1, 1 ).                          % База рекурсии, ограничение вычислений
factorial( N, R ):– N > 0,             % Правило с рекурсией
N1 = N - 1,
factorial( N1, R1 ),
R = R1 * N.
Goal
factorial( 8, F), write( F ).                      % Пример вычисления 8!
При каждом вызове дизъюнкта  factorial  генерируются новые переменные, которые действуют всегда только на своем уровне вложенности, пока не встретится условие прекращения вычислений (базовое правило). Только после этого на обратном пути прохождения рекурсии определяются результаты, которые передаются наверх.
Считается, что используется хвостовая рекурсия, если последнее условие в последнем правиле является рекурсивным. Такая рекурсия имеет преимущество перед нехвостовой рекурсией, так как позволяет ограничить рост стека и строго контролировать процесс возврата. По сути, хвостовая рекурсия - это итеративный процесс. В приведенном примере вычисления факториала рекурсия нехвостовая, а отношения above - хвостовая.

Упражнения

1. Постройте базу данных, отражающую иерархию какой-либо организации: воинской части, научного учреждения, производства. Определите отношения главенства, подчиненности и смежности.
2. Определите рекурсивное отношение НОД (наибольший общий делитель), руководствуясь следующими условиями. Если заданы два целых числа X и Y, то  наибольший общий делитель D определяется правилами:
(1) Если X и Y равны, то D равен X.
(2) Если X > Y, то D равен наибольшему общему делителю X и разности Y – X.
(3) Если X < Y, то формулировка аналогична правилу (2), если X и Y поменять местами.
3. Определите рекурсивный предикат между(N1, N2, X), который с помощью перебора порождает все целые числа X, отвечающие условию N1 <= X <= N.

3.3. Программирование циклических процессов

На языке Пролог могут быть реализованы различные алгоритмические методы позволяющие добиваться того же эффекта, что и в процедурных языках. Самый простой способ управления последовательностью алгоритмов – потребовать, чтобы алгоритм проверял факты и правила в том порядке, в котором они записаны в базе знаний. Пример разветвляющегося алгоритма мы видели в программе решения квадратного уравнения.
Наибольший интерес представляют циклические алгоритмы, поскольку все задачи поиска предполагают многократное повторение одних и тех же действий. Выбор циклического алгоритма зависит от того, как представлены данные, которые требуется обрабатывать. Если данные представлены в виде списка (или рекурсивной структуры иного вида), то оптимальным является применение рекурсивного алгоритма. Если же имеется информация в виде базы данных, содержащей факты, то потребуется использовать алгоритм поиска с возвратом (бэктрекинг). И тот, и другой тип цикла можно реализовать с заданным числом повторений или потенциально бесконечным. Рассмотрим простые примеры всех этих видов циклов.
1. Рекурсивный цикл со счетчиком. Цикл выполнится 10 раз.
for( 10 ).
for( N ) :– N < 10,
prosess,
N1 = N + 1,
for( N1 ).
Goal for( 0 ).
Такой цикл можно использовать, например, для табулирования функции. Табулирование функции - классический пример циклического процесса с заданным числом повторений. Значения функции вычисляются на интервале [0,9] с шагом 1.
Predicates
power( integer )
Clauses
power( 10 ).                               % Базовое правило
power( X ) :-  X < 10,
Y = exp( X * ln( 2 )),              % Здесь табулируемая функция
write( X, Y, '\n' ),
X1 = X + 1,
power( X1 ).
Goal  makewindow( 1, 2, 3,"Power of two", 0, 0, 25, 80 ),
powre( 0 ).
3. Бесконечный рекурсивный цикл. Выполняется ввод и печать символов. Процесс повторяется до нажатия клавиши ENTER, имеющей кодовое число 13.
typewr( '\13' ).
typewr( Char ):– write( Char ),
readchar( C ),
typewr( C ).
Goal readchar( Char ), typewr( Char ).
3. Использование бэктрекинга для перебора всех вариантов. Вспомним, что бэктрекинг есть возврат к поиску других решений, если текущая цель завершилась ложно. В нашем алгоритме ложь «обеспечит» стандартный предикат fail. Пусть есть фрагмент программы:
fact( f1 ).
fact( f2 ).
fact( f3 ).
print_fact :– fact( X ),
write( X ),                                         %  Вывод на экран названия страны
fail.                                                  %  fail – встроенный предикат, означает «ложь»
print_fact.
После того, как будет получен очередной факт  fact(X) и выведен на экран, предикат fail завершит программу ложно, что побуждает поиск других решений. Наличие второго клоза предиката print_fact позволяет всей программе завершиться успешно после печати всех фактов. Надо стремиться, чтобы программа на Прологе всегда завершалась на «истина».
В конкретном примере видим использование бэктрекинга для получения всех решений. Предикат-факт  country  содержит сведения о названии страны и населении. Программа выдает список стран, население которых превышает 1е7.
Predicates
country( symbol, real )
print_countries
Clauses
country( england , 3e7 ).
country( france , 2.3e7 ).
country( germany , 1.6e7 ).
country( denmark , 2.4e6 ).
country( canada , 7.3e6 ).
country( chile, 2.5e ).
print_countries :-
country( X, P ),          %  рассматривается очередной факт
P > 1e7,
write( X ),                 
nl,                             %  перевод строки
fail.              
print_countries.
Goal  print_countries.
После того, как выведен на экран очередной результат, стандартный предикат fail завершает работу предиката print_countries ложно и побуждает Пролог к поиску других решений. Когда будут найдены все решения, второй клоз предиката  print_countries  позволит программе завершиться истинно.
4. Большую группу примеров циклов можно продемонстрировать с использованием предиката  repeat. Этот предикат программируется следующим образом:
repeat.
repeat :– repeat.
Repeat – это цель, которая всегда успешна. Она недетерминирована, это означает, что всякий раз, когда до нее доходит перебор, порождается новая ветвь вычислений.
Пример цикла с сочетанием repeat и fail.
run:– repeat,
readln( X ),
prosess( X, Y ),
write( Y ),
fail.
Предикат fail заставляет систему осуществлять возврат к repeat и prosess в случае успешного завершения. Поскольку это цикл действительно бесконечный, следует предусмотреть в теле цикла возможность выхода из него. Один из способов сделать это – использовать стандартный предикат exit. Эти приемы продемонстрируем при программировании небольшого меню к программе.
Небольшое меню требуется в программах, запускающих различные процессы обработки данных. Такое меню представляет бесконечный цикл, куда каждый раз передается управление после выполнения очередного процесса. Этот цикл можно организовать сочетанием предикатов repeat - fail. В примере, приведенном ниже, сначала создается окно во весь экран, затем открывается цикл. Окно очищается, в нем создается небольшое окно, в котором перечисляются пункты меню. Предполагается, что пользователь введет одну из цифр, от 1 до 5, после чего запускается выбранный процесс. Обращение к стандартному предикату readchar( _ ) вызовет задержку экрана.

clauses
run :- makewindow( 1, 2, 3,"Main Window", 0, 0, 25, 80 ),
repeat,
clearwindow,
write(" select option by number"),
makewindow( 2, 7, 9,"My Menu", 0, 0, 15, 30),
write("1. Consultation\n"),
write("2. Load knowledge\n"),
write("3. Update knowledge\n"),
write("4. Help Information\n"),
write("5. Exit"),
cursor( 0, 0 ),
readchar( C ),
removewindow,
do_choice( C ),
fail.
do_choice( '1' ):- prosess1, readchar( _ ).
do_choice( '2' ):- prosess2, readchar( _ ).
do_choice( '3' ):- prosess3, readchar( _ ).
do_choice( '4' ):- prosess4, readchar( _ ).
do_choice( '5' ):- exit.                                             % Выход из программы
Goal run.
Отметим, что предикаты run, repeat, do_choice не являются стандартными, а пользовательскими, и, следовательно, нуждаются в описании в секции predicates.
Можно также использовать сочетание repeat и стандартного предиката keypressed (вместо repeat – fail) или сочетание not(keypressed) и рекурсии:
run:– repeat,
prosess,
keypressed.
run:– not( keypressed ),
prosess,
run.
С использованием предиката repeat можно также организовать любое подходящее условие окончания работы цикла:
run:– repeat,
prosess,
write("Будет еще ввод? (y/n)" ),
readchar( Ans ),
Ans = 'n'.

3.4. Работа со списками

Списки относятся к структурным объектам Пролога.
Список можно представить как агрегат данных «в ширину», а структуры – «в глубину».
Список в Прологе представляет собой последовательность элементов. Элементами списка могут быть объекты любой природы: числа, строки, символы; простые и составные элементы и сами списки. Список – это структура данных, широко используемая в нечисловом программировании. Для работы со списками используются две фундаментальные операции. Первая из них возвращает первый элемент списка, вторая возвращает список, полученный после удаления первого элемента.  
Списки являются одной из основных структур данных Пролога. Список является в некотором смысле аналогом массива в алгоритмических языках программирования. Однако здесь есть существенные отличия. Основным механизмом работы со списками является рекурсия, позволяющая компактно описывать алгоритмы. Для рекурсии не требуется знания точного числа элементов списка, достаточно определения, как правило, головного элемента списка и условия окончания работы рекурсии. Поэтому элементы списков не индексируются, соответственно, количество элементов списка не фиксируется. Фундаментальные операции наряду с рекурсией составляют основу высокоуровневых алгоритмов работы со списками. 
Можно также провести аналогию списков Пролога и динамических однонаправленных списковых структур языка Паскаль. От последних их выгодно отличает отсутствие необходимости работать с адресной частью списков.
Для удобства обработки списков в Прологе введены два понятия: голова и хвост. Первый элемент списка (или несколько первых элементов) являются головой списка, а оставшиеся – его хвостом. Тогда список – это структура данных, определяемая следующим образом:
– список является либо пустым,
– либо состоящим из головы и хвоста; головой списка может быть элемент любого типа, а хвост должен быть, в свою очередь, списком.
Видно, что это определение является рекурсивным: понятие списка определяем через сам же список. Здесь же намечается механизм обработки списка: выделить в списке головной элемент и выполнить с ним требуемые действия (например, распечатать), далее продолжить те же самые действия с оставшейся частью списка, т.е. хвостом. Действия выполняются до тех пор, пока не сработает операция останова, а она содержится в нерекурсивной части определения, т.е. до тех пор, пока список не станет пустым.
Для обозначения списка используются квадратные скобки, а для отделения головы списка от его хвоста – символ "|". Например, для списка [1 | 2, 3] элемент 1 является головой, а список [2, 3] хвостом. Пустой список обозначается [ ]. Если список не разделяется на голову и хвост, квадратные скобки можно опустить.
Списки можно применять для представления множеств. Некоторые операции над списками примерно те же, что и над множествами:

• Проверка, является ли некоторый объект элементом списка
• Объединение, пересечение, разность двух списков
• Добавление некоторого объекта в список или удаление некоторого объекта из него.

3.4.1. Описание списков в программе

Для указания Прологу того, что мы предполагаем использовать списки в программе, используется второй формат указания Domains:
mylist = elevent* ,
где mylist – объявление списка элементов,  element – один из стандартных типов Турбо-Пролога, либо ранее описанный пользователем в Domains;  “*” – обязательный элемент синтаксиса, обозначает список. Например, домен
namlist = integer*
объявляет список целых чисел. Таким образом, шапка программы для работы со списком:
Domains
namlist = integer *
Predicates
add( integer, namlist, namlist )  % Объявляем предикат добавления элемента в список
Clauses
/* Далее следуют клозы предиката  add */
Рассмотрим некоторые предикаты для обработки списков.
3.4.2. Добавление элемента в список
Требуется запрограммировать предикат add (добавить). Он должен иметь три аргумента: добавляемый элемент X,  исходный список L и L1 - результирующий список:
add ( X, L, L1).
Поскольку речь не идет о том, что элемент требуется поставить на некоторое определенное место, то наиболее простой способ добавить элемент в список – это вставить его в самое начало так, чтобы он стал новой головой. В этом случае предикат имеет самый простой вид, можно обойтись без рекурсии. Если X – это новый элемент, который добавляют в список L, то предикат добавления элемента в список запишется следующим образом:
add( X, L, [ X | L ] ).
Отношение add можно использовать в обратном направлении для того, чтобы удалить голову списка. Заметим, что особенность работы предикатов Пролога «в обе стороны» является широко эксплуатируемой и представляет приятную неожиданность в декларативном программировании. Как же Пролог узнает, что делать со списком: отсекать ему голову или, наоборот, добавлять? На это вопрос легко ответить, если вспомнить основной вычислительный механизм Пролога: сопоставление и унификация. Если, например, встретится цель
Goal add( 5, [ 3, 6, 1], L ),
в которой третий аргумент не конкретизирован, то согласно реализации предиката add будет выдан ответ:
L= [ 5, 3, 6, 1 ].
Если же будет задана цель, в которой первый и третий аргументы конкретизированы, а второй – нет, Пролог конкретизирует его опять таки согласно алгоритму добавления, но с точностью наоборот:
Goal add( 5, L, [ 5, 3, 6, 1 ] ).
L = [ 3, 6, 1 ].
Если первый аргумент нас не интересует, вместо него можно указать анонимную переменную, тогда цель будет выглядеть еще проще (с тем же результатом):
Goal add( _ , L, [ 5, 3, 6, 1 ] ).
3.4.3. Удаление элемента
 Удаление элемента X из списка L можно определить в виде отношения
away( X, L, L1 ),
где L1 – это список L, из которого удален элемент X.
Поскольку заранее не известно, где находится в списке удаляемый элемент, без рекурсивного перебора списка не обойтись.
Определим отношение  away  с использованием рекурсии следующим образом: если X является головой списка, тогда результатом удаления будет хвост этого списка T (первое правило, без рекурсии). Иначе, если X не совпадает с головой списка, т.е. находится в хвосте списка, тогда его нужно оттуда удалить:
away( X, [  X | T ], T ).
away( X, [ Y | T], [ Y | T1 ] ):– away( X, T, T1 ).
Если в списке встречается несколько вхождений элемента X, то away сможет исключить их все при помощи возвратов. Вычисление по каждой альтернативе будет удалять лишь одно вхождение X, оставляя остальные в неприкосновенности. Например:
goal away ( 5, L, [ 5, 3, 5, 6, 1, 5 ],).
L = [ 3, 5, 6, 1, 5 ].
L = [ 5, 3, 6, 1, 5 ].
L = [ 5, 3, 5, 6, 1 ].
При попытке исключить элемент, не содержащийся в списке, отношение away неудачу.
Отношение away можно использовать в обратном порядке для того, чтобы добавлять элементы в список, вставляя их в произвольные места. Операция по внесению X в произвольное место некоторого списка Spisok, дающее в результате больший список Bolsh_spis, может быть определена предикатом add2:
add2( X, Spisok, Bolsh_spis ):-
away ( X, Bolsh_spis, Spisok).
3.4.4. Принадлежность элемента списку
Требуется определить предикат:
member(X,L).
Здесь L – некоторый список, Х – объект того же типа, что и элементы списка L. Составление предиката может быть основано на следующих соображениях: X есть либо голова списка L, либо X принадлежит хвосту. Это может быть записано в виде двух предложений, первое из которых есть простой факт, ограничивающий вычисления, а второй – рекурсивное правило:
member(X, [X| _ ]).
member(X, [ _ | T ]):– member(X,T).
Напомним, что знаком подчерка здесь обозначена анонимная переменная, значение которой в данном предложении неважно.
Работа предиката следующая: при каждом рекурсивном вызове список будет короче, т.к. аргументом заголовка является структура [ _ | T ], а в рекурсивном вызове - список Т. Рекурсивные вызовы продолжаются до тех пор, пока не будет достигнуто совпадение значения переменной X с головой списка Т, или если окажется пустой список, тогда предикат завершается ложно, так как для пустого списка нет своего правила.
Обычно этот предикат используют в двух вариантах:
1) Переменная X неконкретизирована, а список L конкретизирован. В этом случае в результате работы предиката переменная X конкретизируется элементом списка L. Используя механизм возвратов, можно переменной X последовательно придавать значения всех элементов списка L.
2) Переменная X и список L конкретизированы. Значением предиката будет “истина”, если X совпадает с одним из элементов списка, и "ложь" в противном случае.
Для проверки на принадлежность можно также использовать и отношение «удалить»: некоторый X принадлежит списку, если его можно оттуда удалить:
member( X, L ) :- away( X, L, _ ).
При этом элемент X вовсе не удаляется из списка L, достаточно только того, чтобы существовала возможность его удаления, т.е. предикат away должен закончиться на «истинно».
3.4.5. Сцепление (конкатенация) списков
Определим предикат
conc( L1, L2, L3 ).
Объединяемые списки задаются первыми двумя аргументами L1 и L2. Список L3 представляет собой конкатенацию этих списков.
Для определения отношения конкатенация отделим два случая:
(1) Если первый список пуст, то второй и третий представляют собой один и тот же список (базовое правило):
conc( [ ], L , L ).
(2) Если первый аргумент не пуст, то он имеет голову и хвост, т.е. [X|L1]. Его сцепление со списком L2 – список [X|L3], где список L3 получен после сцепления списков L1 и L2, т.е.
conc( [ X | L1 ], L2, [ X | L3 ] ) :– conc( L1, L2, L3 ).
На первый взгляд далеко не очевидно, почему, к примеру, в базовом правиле первый список должен быть пуст, а не второй. Однако дело прояснится, если вспомним, что правила Пролога имеют не только декларативный, но и процедурный смысл. А именно он сейчас важен. Второе правило с рекурсией раскрывает механизм конкатенации: из первого списка элементы перекачиваются во второй, становясь каждый раз его головой; процесс продолжается, пока первый список не опустеет. В этот момент сработает базовое правило, третий список конкретизируется вторым аргументом. Далее начнется обратное прохождение рекурсии, элементы по одному будут возвращаться в первый и третий аргументы до тех пор, пока не закончатся возвраты рекурсии.
Познакомимся с механизмом рекурсивного вызова процедур  на конкретном примере. Пусть требуется выполнить конкатенацию списков [a,b] и [c,d]. Таким образом, первый и второй аргументы конкретизированы, а третий еще нет. Начинается прямое прохождение рекурсии: по правилу (2):
conc([a, b], [c, d], L3),
где L3 есть конкатенация элемента  а  и некоторого списка L31,  т.е. L3=[a | L31]. Этот предикат вызывает
   conc([b], [c, d], L31),
где L31=[b | L311], далее вызывает
                   conc([ ], [c, d], L311).

Здесь L3, L31, L311 - сгенерированные переменные, обозначающие еще неконкретизированные списки.
По базовому правилу (1) последнее отношение удовлетворяется, если L311 конкретизируется списком [c,d]. Теперь начинается обратное прохождение рекурсии, при котором конкретизируются списки L1,L:
              conc([ ], [c, d], [c, d]),     возвращает
  conc([b], [c, d], [b, c, d]),    возвращает
conc([a,b], [c, d], [a, b, c, d]).

Таким образом, базовое правило имеет декларативный и процедурный смысл. Декларативный аспект был указан ранее. Процедурное значение этого правила в том, что оно дает ограничение рекурсии и конкретизирует последнюю сгенерированную переменную (результат).
Отношение конкатенации можно использовать многими способами. Например, его можно применять в обратном направлении для разбиения заданного списка на две части:
Goal conc( L1, L2, [ a, b, c ]).  
L1 = [ ]
L2 = [ a, b, c ]  
L1 = [ a ]
L2 = [ b, c ]  
L1 = [a, b]
L2 = [ c ]  
L1 = [a, b, c ]
L2 = [ ]  
Это отношение также можно применить для поиска в списке элементов, отвечающих некоторому условию, задаваемому в виде образца (шаблона). Например, можно найти все элементы, предшествующие данному и все следующие за ним, сформулировав вопрос:
Goal conc( L1, [ c | L2], [ a, b, c, d, e, f ] ).   
L1 = [ a, b ]
L2 = [ d, e, f ]   
Далее, мы сможем, например, удалить из некоторого списка L1 все, что следует за тремя последовательными вхождениями элемента z  в L1 вместе с этими тремя z:
Goal L1 = [ a, b, z, z, c, z, z, z, d, e, f ] ,   
conc( L2 , [z, z, z | _ ], L1).   
L1 = [ a, b, z, z, c, z, z, z, d, e, f ] ).   
L2 = [ a, b, z, z, c ] ).   
Через конкатенацию можно определить отношение «последний элемент списка» last так, чтобы элемент E являлся последним элементов списка L:
last( E, L ) :- conc( _ , [ E ], L ).
Мы уже запрограммировали два раза отношение принадлежности. Однако, используя конкатенацию, можно было бы определить это отношение следующим способом:
member( X, L ):-
conc( _ , [ X | _ ], L ).
В этом предложении сказано: «X принадлежит L, если список L можно разбить на две части таким образом, чтобы элемент X являлся головой второго их них».
Рассмотрим теперь отношение «подсписок» (sub_list). Это отношение имеет два аргумента – список L и список S такой, что S содержится в L в качестве подсписка. Так, отношение
sub_list( [ c, d, e ], [a, b, c, d, e, f ])
имеет место, а отношение
sub_list( [ c, e ], [a, b, c, d, e, f ])
нет. Его можно сформулировать так:
(1) L можно разбить на два списка L1 и L2 и
(2) L2 можно разбить на два списка S и L3. Поскольку в данном случае неважно, какой останется L3, вместо него поставим анонимную переменную
Поэтому вышеприведенную формулировку можно выразить на Прологе так:
sub_list( S, L ):-
conc( L1, L2, L ),
conc( S, _ , L2 ),
3.4.6. Удаление из списка повторяющихся элементов
Аргументами предиката unik являются два списка: исходный и результирующий. Смысл алгоритма прост: если элемент присутствует в списке (проверяется предикатом member), то он не записывается в результирующий  список, иначе добавляется в качестве головного элемента.
unik ( [ ], [ ] ).
unik( [ H | T ], L ):– member( H, T ), unik( T, L ).
unik( [ H | T], [ H | L ] ):– unik( T, L ).
3.4.7. Вычисление суммы элементов списка
Можно выполнить предикатом
sum( L, S ).
Здесь S – сумма элементов числового списка L. Запрограммировать этот предикат можно двумя способами. Рассмотрим сначала более очевидный (но не более простой для Пролога):
sum( [ ], 0 ).
sum( [ H | T ], S1 ):–
sum( T, S2 ), S1 = S2 + H.
Декларативный смысл этого алгоритма: если список пуст, то сумма его элементов равна нулю, иначе, если список не пуст, его можно разделить на голову H и хвост T; сумма элементов такого списка S1, при этом сумма элементов хвоста  T  есть  S2  и  S1=S2+H. Обратим внимание, что это рекурсия нехвостовая: в рекурсивном правиле предиката  sum  рекурсивное условие записано не последним. Нехвостовая рекурсия при последовательных вызовах генерирует промежуточные переменные, которые конкретизируются при обратном прохождении рекурсии.
Поясним работу этого предиката на примере. Пусть требуется найти сумму элементов списка [3,6,1]. Последовательность рекурсивных вызовов и возвратов следующая:
sum( [ 3 | 6, 1], S )  вызывает   sum([6,1],S1) и S=S1
sum([6|1],S1)   вызывает   sum([1],S11)  и S1=S11+6.
sum([1],S11)    вызывает   sum([ ],S111)  и S11=S111+1.
sum([ ],S111)  удовлетворяется, если S111 конкретизируется 0.
sum([1],S11)    удовлетворяется, если S11 конкретизируется 1.
sum([6,1],S1)   удовлетворяется, если S1 конкретизируется 7.
sum([3,6,1],S)  удовлетворяется, если S конкретизируется 10.
Другой алгоритм вычисления суммы не так нагляден, но он позволяет отменить нехвостовую рекурсию.
sum( L, S):– sum1( L, 0, S ).
sum1( [ ], S, S ).                         % Базовое правило, список пуст, сумма накоплена
sum1( [ H | T ], S1, S ):–
S2 = S1 + H,
sum1( T, S2, S ).
Здесь используем тот же прием, что и в предикате обращения списка: используем более общий предикат sum1, имеющий дополнительный аргумент S, в котором зафиксируется результат. Декларативный смысл базового правила: если список исчерпан, то сумма накоплена, при этом конкретизируется третий аргумент.
Тот же пример:
sum1( [ 3 | 6, 1 ], 0, S)   вызывает   sum1( [ 6, 1 ], 3, S).
sum1( [ 6 | 1], 3, S)    вызывает   sum1( [ 1 ], 9, S).
sum1( [ 1 ], 9, S)    вызывает   sum1( [ ], 10, S).
sum( [ ], 10, S)   удовлетворяется, если S  конкретизируется 10.
Последовательность возвратов следующая:
sum1( [ 1 ], 9, 10)
sum1( [ 6, 1], 3, 10)
sum1( [ 3, 6, 1 ], 0, 10)
Таким образом, здесь имеем итеративный процесс, на каждом шаге которого все переменные имеют конкретные значения; нет необходимости в генерации промежуточных переменных, соответственно алгоритм контролирует рост стека. Кроме того, мы видим, что после завершения работы алгоритма первый и второй аргументы предиката sum1 получили свои первоначальные значения, поскольку были конкретизированы, поэтому наличие третьего аргумента, первоначально не конкретизированного, обязательно: он фиксирует результат.
3.4.8. Обращение списка
Определим предикат
reverse( L1, L2 ).
Аргументы L1 и L2 – два списка, из которых список L2 содержит элементы списка L1, записанные в обратном порядке.
reverse( L1, L2 ):– reverse1( L1, [ ], L2 ).
reverse1( [ ], L, L ).
reverse1( [ H | T ], L1, L2 ):– reverse1( T, [ H | L1 ], L2 ).
Предикат  reverse  в данном случае является интерфейсным, он  запускает в работу основной рабочий предикат reverse1,  имеющий дополнительный второй аргумент – список, который вначале пуст, и используется собственно для обращения списка. На каждом шаге рекурсии один элемент исходного списка становится головой промежуточного списка. Третий аргумент передается от шага к шагу и конкретизируется в момент достижения базового состояния предиката reverse1. Когда первый список исчерпан, второй уже содержит элементы, записанные в обратном порядке. Отметим, что наличие третьего аргумента, фиксирующего результат, обязательно, т.к. после обратного прохождения рекурсии все конкретизированные переменные принимают свои первоначальные значения. Проследить работу этого предиката можно, если его расписать, как в предыдущем примере.

3.4.9. Нахождение максимального элемента списка
Здесь нам понадобится вспомогательный предикат max, выбирающий максимальное значение из двух элементов:
max( X, Y, X ):–  X >= Y.
max( X, Y, Y ):–  X < Y.
Результативный предикат maxlist(LIST, MAX), где MAX – наибольший элемент списка LIST, выглядит следующим образом:
maxlist( [ X ], X ).
maxlist( [ X, Y | TAIL ], MAX ) :–
maxlist( [ Y | TAIL ], MAXTAIL ),
max( X, MAXTAIL, MAX ).
Смысл базового правила: максимальный элемент одноэлементного списка равен самому этому элементу. Иначе, если в списке есть хотя бы два элемента X и Y, выбирается максимальный элемент хвоста MAXTAIL и при этом MAX равен наибольшему из X и MAXTAIL. Рекурсия здесь нехвостовая, чтобы обеспечить конкретизацию переменных  X  и  MAXTAIL.
3.4.10. Перестановки
В различных логических задачах часто требуется строить перестановки элементов некоторого заданного списка. Для этого определим отношение permutation двумя аргументами. Аргументы – это два списка, один из которых является перестановкой другого.
Программирование отношения permutation основывается на рассмотрении двух случаев:
(1) Если первый список пуст, то и второй список должен быть пустым.
(2) Если первый список не пуст, тогда он имеет вид [ X | L ], и перестановку такого списка можно построить так: вначале получить перестановку списка L1, а затем внести X в произвольную позицию L1.
Два прологовских предложения, соответствующие этим случаям, таковы:
permutation ( [ ], [ ] ).
permutation ( [ X | L ], P ) :-
permutation ( L, L1 ),
add2( X, L1, P ).
Программирование отношения permutation можно реализовать и другим способом, если вспомнить, что отношение «внести» программируется через «удалить».

3.4.11.                    Примеры использования списков

Программирование рекурсивных предикатов работы со списками как основными структурами данных представляет собой увлекательное занятие.
Пролог идеально подходит для решения различного рода математических ребусов и головоломок, требующих перебора. При этом пространство состояний удобно представлять в виде списков, из которого можно «черпать» элементы. Рассмотрим одну такую головоломку.
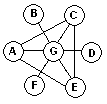Требуется расставить в кружочках числа от 1 до 25 таким образом, чтобы каждая сумма по каждой диагонали была равна 25 и сумма вершин треугольника тоже бы равнялась 25. Разным буквам должны соответствовать разные числа, иначе возможно тривиальное решение.
Список чисел, из которого будут конкретизироваться переменные, определим как факт cifr. Введем отношение summa, аргументами которого будут семь переменных, которые предстоит конкретизировать с выполнением заданных условий. В программе действия по конкретизации переменных выполняет предикат удаления элемента из списка away. Это трехаргументное отношение, в котором в нашем примере конкретизирован второй аргумент – список доступных чисел. Предикат конкретизирует число из этого списка и возвращает третий аргумент – список без удаленного числа. Путем последовательных удалений будут конкретизированы все числа.
Полная программа для решения головоломки приводится ниже.
Domains
i = integer
ILIST= i *
predicates
summa( i, i, i, i, i, i, i, ILST )
away( i, ILIST, ILIST )
cifr( ILIST )
clauses
cifr([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]). % Столько чисел хватит
summa( A, B, C, D, E, F, G, CIF ) :-
away( A, CIF, CIF1 ),
away( B, CIF1, CIF2 ),
away( C, CIF2, CIF3 ),
away( D, CIF3, CIF4 ),
away( E, CIF4, CIF5 ),
away( F, CIF5, CIF6 ),
away( G, CIF6, _ ),
A + G + D = 25,
B + G + E = 25,
C + G + F = 25,
A + C + E = 25.
away( A, [ A | L ], L ).
away( A, [ B | L ], [ B | L1 ] ):-
away( A, L, L1 ).
goal cifr( CIF ),                   % Переменная CIF конкретизируется списком чисел
summa( A, B, C, D, E, F, G, CIF ), write( A, B, C, D, E, F, G ).
В данном случае у нас найдено только одно решение. Для получения всех решений следует включить бэктрекинг (см. «Организация циклов»).

Упражнения

1. Стандартный предикат вывода write выводит список «в строку». Запишите рекурсивный предикат вывода списка на экран а) «в столбец»; в) в виде таблицы по пять элементов в строке.
2. Список целых чисел иногда удобно представить в виде диаграммы. Пусть  процедура diagramma выводит список в такой форме:
Goal diagramma( [ 3, 4, 6, 5 ] ).

* * *
* * * *
* * * * * *
* * * * *
Определите рекурсивную процедуру diagramma.
Указание. Для вывода заданного количества звездочек в строке используйте рекурсивный цикл со счетчиком.
2. Выборка упорядоченных пар из двух списков. Определим отношение much с четырьмя аргументами:
         much( X1, X2, L1, L2 ).
Аргументы X1, X2 - это элементы соответственно списков L1 и L2, стоящие в своих списках в одной и той же позиции. Списки L1 и L2 одинаковой длины.
3. Упражнения на конкатенации. 103 Бр Определить отношение «последний» без использования конкатенации. Определите отношение «сдвиг» с использованием конкатенации 110 Бр
4. Список может представлять собой множество. Над списками выполняются такие операции как добавление, удаление, пересечение, разность, равенство. Выясните, какие предикаты из рассмотренных ранее могут представлять операции над списками. Допишите необходимые предикаты.

3.5. Виды рекурсии

Теперь, когда мы разобрали работу множества рекурсивных предикатов, можно подробнее разобраться с видами рекурсии, как основного механизма организации вычислительного процесса в задачах поиска.
Рекурсии в Прологе бывают нескольких видов:

• Простая
• Взаимная
• Вложенная
• Параллельная.

Многочисленные примеры простой рекурсии мы уже рассмотрели. Это может быть рекурсия хвостовая и нехвостовая, но содержащая только однократный рекурсивный вызов в теле предиката. Это предикаты вычисления суммы элементов списка, конкатенации, принадлежности элемента списку, нахождения максимального элемента списка и др.
Для демонстрации взаимной рекурсии определим два предиката:
chet ( L ) и nechet ( L ),
таким образом, чтобы они были истинны, если их аргументом является список четной или нечетной длины соответственно.
chet ( [ ] ).                           % Пустой список имеет четную длину
chet ( [ _ | T ] ):- % Список четной длины, если хвост - нечетной
nechet ( T ),
nechet ( [ _ ] ). % Список из одного элемента имеет нечетную длину
nechet ( [ _ | T ] ):-             % Список нечетной длины, если хвост - четной
chet ( T ).

 Пример вложенной рекурсии – предикат unik, удаляющий из списка повторяющиеся элементы: помимо рекурсивного вызова, он содержит вызов другого рекурсивного предиката – member.  Очевидна организация вложенного циклического процесса:        
unik( [ ],[ ] ).
unik([ H | T ], L):– member( H,T), unik( T,L).
unik([ H | T ], [ H | L ]):– unik(T, L).
Параллельную рекурсию продемонстрируем на примере алгоритма, реализующего так называемую быструю сортировку Хоара. Идея этого алгоритма:
(1) Удалить из списка L первый элемент X и разбить оставшуюся часть на два списка, называемые следующим образом: все элементы, меньшие чем X, принадлежат списку  Mensh, остальные - списку Bolsh.
(2) Отсортировать список Mensh, результат – Upor_Mensh.
(3) Отсортировать список Bolsh, результат – Upor_Bolsh.
(4) Получить результирующий упорядоченный список как конкатенацию списков Upor_Mensh и
[X|Upor_Bolsh].
Заметим, что если исходный список пуст, то и результатом сортировки тоже будет пустой список. Разбиение на два списка запрограммировано как отношение с четырьмя аргументами:
razbienie(X, L, Mensh, Bolsh).
Программа записана ниже.
sortirovka( [ ],[ ] ).
sortirovka( [ X|T ], Upor_spis ):-
razbienie(X, T, Mensh, Bolsh ),
sortirovka( Mensh, Upor_Mensh ),
sortirovka( Bolsh, Upor_Bolsh),
conc(Upor_Mensh, [X|Upor_Bolsh], Upor_spis).
razbienie( _ , [ ], [ ], [ ]).
razbienie( X, [Y|T ], [Y| Mensh], Bolsh):-
X>Y, !, razbienie( X , T, Mensh, Bolsh ).
razbienie( X, [Y|T ], Mensh, [Y| Bolsh]):-
razbienie( X, T, Mensh, Bolsh):-
Параллельность сортировки – рекурсивный предикат sortirovka дважды вызывает сам себя в правой части правила.

3.6. Поиск в пространстве состояний

Рекурсия – это естественный способ реализации таких стратегий искусственного интеллекта, как поиск на графе. Поиск в пространстве состояний – процесс, рекурсивный по природе.
Для широкого класса задач ИИ имеется одна общая схема для представления задач, называемая поиском в пространстве состояний. Пространство состояний – это граф, вершины которого соответствуют ситуациям, встречающимся в задаче («проблемные ситуации), дуги соответствуют разрешенным переходам из одного состояния в другое. Если пространство состояний невелико, его можно задать явным способом, перечислив все дуги графа. В противном случае требуется разработать некоторый общий оператор перемещения из одного состояния в другое, т.е. так называемый генератор состояний.
Решение задачи сводится к поиску пути между заданной начальной ситуацией (стартовой вершиной) и некоторой заранее указанной конечной ситуацией, называемой целевой вершиной. При этом возникает проблема, как обрабатывать альтернативные пути поиска: либо в первую очередь обрабатывать наиболее далекие вершины, либо ближайшие к стартовой.  
Когда происходит поиск пути на графе, граф разворачивается в дерево, причем некоторые пути, возможно, дублируются. Корнем такого дерева является стартовая вершина, листьями – целевая либо тупиковая вершины.
Рассмотрим карту городов и соединяющих их дорог.

Рис. а) карта городов и дорог; б) дерево поиска
Пусть a – стартовая вершина, z – целевая вершина. Карта может использоваться для поиска всех маршрутов из а в z. Когда известно стартовое и конечное состояние, компьютер разворачивает карту дорог в виде дерева, где корень дерева представляет стартовую вершину, а листья – целевые вершины либо тупики. Дерево показывает все варианты пути. Дороги либо приводят в тупик, либо заканчиваются в z. (Заметим, что при построении этого дерева мы «автоматически» не рассматривали петли. Так, из вершины c можно попасть в g, а из g снова в е – получается петля).
Подходящее дерево поиска создается обычно при решении любой задачи поиска. Оно обычно разворачивается постепенно в процессе самого поиска. Мы будем представлять пространство состояний при помощи отношения
posle ( X, Y ),
которое истинно тогда, когда в пространстве состояний существует разрешенные переход из вершины X в вершину Y:
posle ( a, b ). 
posle ( a, c ). 
posle ( b, d ). 
posle ( b, e ).
posle ( c, f ). 
. . .
Следующая задача состоит в построении алгоритма поиска для определения пути последовательных шагов.
Какую стратегию применять машине? Человек сразу же выбрал подходящую дорогу, но компьютер на это не способен. При отсутствии прочей дополнительной информации компьютер использует для поиска стратегию «грубой силы»:  программа осуществляет поиск, идя от состояния к состоянию и систематически исследуя все возможные пути. Существует две основных стратегии перебора альтернатив, а именно, поиск в глубину и поиск в ширину.
Поиск «в глубину» означает тот порядок, в котором рассматриваются альтернативы в пространстве состояний. Реализация метода соответствует обходу дерева в глубину, при этом встречаемые вершины заносятся в стек. Когда требуется продолжить поиск, из стека извлекается последняя занесенная в него вершина, т.е. наиболее «глубокая» (расположенная дальше других от стартовой). Говорят, что вершина раскрывается, т.е. к ней применяются все подходящие подстановки.

Метод прост в реализации, поскольку наиболее адекватен принятой в Прологе стратегии обработки подцелей «в глубину». Разработка алгоритма основана на следующей идее:

• Если B – это целевая вершина, то положить Resh = [ B ];
• Если для вершины B существует вершина-преемник, такая, что можно провести путь Resh1 из B1 в целевую вершину, то положить Resh  = [ B | Resh1 ].

На Прологе это алгоритм транслируется так:
v_glubinu( B, [ B] ) :-
mygoal ( B ).
v_glubinu( B, [ B | Resh1] ) :-
posle ( B, B1 ),
v_glubinu( B1, Resh1 ).
Решение будет получено, если зададим цель:
Goal v_glubinu( a, Resh ), write ( Resh ).
Здесь переменная Resh – величина неконкретизированная, представляющая некоторый список. По мере работы алгоритма на каждом шаге рекурсии этот список становится все короче и короче и в момент достижения базового правила конкретизируется одной вершиной, а именно – целевой. При обратном прохождении рекурсии все пройденные вершины собираются в список, и найденный путь получается в прямом порядке.
Поиск в глубину в некоторых случаях хорошо работает, а именно, если исходный граф вывода изначально представлен в виде дерева, т.е. не содержит циклов. Очевиден недостаток нашей реализации: при изображении дерева выводы мы избегали петель графа, которые присутствуют в исходной карте. В алгоритме же, в котором отсутствует механизм обнаружения петель, существует опасность зацикливания. Поэтому очевидное усовершенствование этого алгоритма – добавление к нему механизма обнаружения циклов. Каждую вершину-кандидата B1 продолжения поиска следует проверять на ее отсутствие в уже накопленном пути Way:
not( member( B1, Way ) ).
 Здесь member – знакомый предикат проверки принадлежности элемента списку.
Поскольку предикат отрицания not требует конкретизированных аргументов, очевидна необходимость начать вычисления от конкретизированного списка (например, пустого) и иметь уже тем больший список, чем больше вложенность рекурсии, т.е. накапливать список в правой части правила. Но в таком случае накопленный список надо зафиксировать в базовом правиле введением дополнительного аргумента:
user_interface( B, Resh ) :-
v_glubinu2( [ ], B, Resh ).
v_glubinu2( Way, B, [ B | Resh ] ) :-
mygoal ( B ).
v_glubinu2( Way, B, Resh ) :-
posle ( B, B1 ),
not( member( B1, Way ) ),
v_glubinu2( [ B | Way ], B1, Resh ).
Для запуска этой программы можно воспользоваться интерфейсным предикатом  user_interface, аргументы которого содержат стартовую вершину и полученное решение.
Goal user_interface( a, Resh ), write ( Resh ).
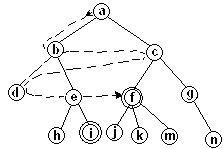 Стратегия поиска в ширину предусматривает переход в первую очередь к вершинам, ближайшим к стартовой. Метод программируется более сложно, так как нужно сохранять множество альтернативных вершин-кандидатов в списке. Реализации метода соответствует занесение пройденных вершин в очередь, реализующую принцип: «первый пришел – первый вышел».
Первоначально список вершин состоит из одной стартовой вершины, далее применяется следующий алгоритм: первый элемент списка удаляется, а в конец списка заносятся дочерние вершины. Удаляемые вершины заносятся в другой список, который в конечном счете и даст решение.
Таким образом, последовательность нахождения вершин в списке следующая:
[ a ] 
[ b, c ] 
[ c, d, e ] 
[ d, e, f, g ] 
[ f, g, h, i ] .
Работа алгоритма продолжается до тех пор, пока целевая вершина не окажется в начале списка.
Такой алгоритм найдет решение кратчайшим путем (если только решение существует).
Поиск в ширину программируется не так легко, как в глубину, поскольку нам приходится сохранять все множество альтернативных вершин-кандидатов, а не только одну вершину, как при поиске в глубину. Кроме того, если мы желаем получить решающий путь, то одного множества вершин не достаточно. Поэтому мы будем хранить не множество вершин-кандидатов, а множество путей-кандидатов. Это множество будет списком путей, а каждый путь – списком вершин, перечисленных в обратном порядке, т.е. головой такого списка будет самая последняя из порожденных вершин, а последним элементом списка будет стартовая вершина. (338Бр)
Поиск начинается с одноэлементного множества кандидатов [[S]] (стартовой вершины, преобразованной в список списков), далее нужно выполнить:

• Если голова первого пути – это целевая вершина, то взять этот путь в качестве решения
• Если это не так, удалить первый путь из множества кандидатов и породить множество всех возможных продолжений этого пути на один шаг; множество продолжений добавить в конец множества кандидатов, а затем выполнить поиск в ширину с полученным новым множеством.

В случае примера на рис. этот процесс будет развиваться следующим образом:
[ [ a ] ] 
[ [ b, a ], [ [ c, a ] ] 
[ [ c, a ], [ d, b, a ], [ e, b, a ] ] 
[ [ d, b, a ], [ e, b, a ], [ f, c, a ], [ g, c, a ] ] 
…
[ [ f, c, a ], [ g, c, a ], [ h, e, b, a ],[ i, e, b, a ], [ j, f, c, a ] ].
Для реализации поиска средствами исчисления предикатов необходим такой режим управления, который осуществляет систематический поиск в пространстве состояний, и при этом позволяет избежать тупиковых путей и зацикливания.
Алгоритм реализуется на Прологе следующей программой:
Domains
list = string *
Llist = list *
Predicates
user_interface ( string, list )
vshir ( Llist, list )
kandidat ( list, list )
conc ( Llist, Llist, Llist )
member ( string, list )
posle ( string, string )
my_goal ( string )
Clauses
posle ( a, b ).  posle ( a, c ).  posle ( b, d ).  posle ( b, e ).
posle ( c, f ).  posle ( c, g ).  posle ( e, h ).  posle ( e, i ).
posle ( f, j ). 
my_goal ( f ).                                                                % Целевая вершина
user_interface ( S, Resh ) :-
vshir ( [ [ S ] ], Resh ).
vshir ( [ [ V | Way ] | _ ], [ V | Way ] ) :-                                % Голова списка – полученное решение
my_goal ( V ).                                                                  % Цель достигнута
vshir ( [ [ V | Way ] | Ways ], Resh ) :-
% New_ways - все продолжения пути на один шаг
findall ( X, kandidat ( [ V | Way ], X ), New_ways ),
conc ( Ways, New_ways, Ways1 ), !,                        % Добавление в конец  множества кандидатов
vshir ( Ways1, Resh );
vshir ( Ways, Resh ).                                    % Продолжение поиска в случае тупикового пути
kandidat ( [ B | Way ], [ B1, B | Way ] ) :-
posle ( B, B1 ),
not ( member ( B1, [ B | Way ] ) ).                             % Обнаружение зацикливания
member ( X, [ X | _ ] ).
member ( X, [ _ | T ] ) :- member ( X, T ).
conc ( [ ], L, L ).
conc ( [ X | L1 ], L2, [ X | L3 ] ) :-
conc ( L1, L2, L3 ).
goal user_interface ( a, Resh ), write ( Resh ).        
Обе эти стратегии  (поиск в глубину и поиск в ширину) обносятся к так называемым алгоритмам полного перебора пространства состояний. Они способны получить оптимальное решение, но время получения решения может оказаться неприемлемым. Более изощренные процедуры поиска используют какую-либо дополнительную информацию, отражающую специфику задачи, с тем, чтобы на каждой стадии поиска принимать решение о наиболее перспективных путях поиска. Дополнительная информация, относящаяся к конкретной решаемой задаче, используемая для управления поиском, называется эвристикой, а алгоритмы, использующие эвристику – эвристическими. Эвристические алгоритмы могут быть реализованы как на базе поиска в глубину, так и в ширину.
Рассмотрим детальную реализацию поиска пути на графе на базе алгоритма поиска в глубину.  После несложного расширения эта программа сможет отвечать на следующие вопросы:
- как добраться из одной вершины в другую, не посещая дважды одной и той же вершины;
- как пройти по маршруту, посетив заданную вершину;
- как добраться до нужной вершины, избежав некоторых вершин.

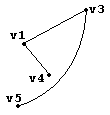
Рис. Граф, представляющий фрагмент пространства состояний
Пусть имеется следующий граф, представляющий фрагмент пространства состояний.
Центральной частью программы будет база данных (факты), содержащая данные о сети дуг между вершинами. Эта информация представлена в виде двухаргументного отношения road, например:
road( v1, v3 ).
road( v4, v1 ).
road( v3, v5 ). 
Необходимо иметь информацию об обратных направлениях. Вместо того, чтобы переписывать факты, воспользуемся правилом road1:
road1( T1, T2 ) :– road( T1, T2 );
road( T2, T1 ).
Для решения этой задачи удобнее всего собирать в список все пройденные вершины. Будем исходить из следующих соображений: если существует дуга из вершины X в вершину Y, то путь найден (базовое правило), иначе чтобы найти путь из X в Y, надо найти дугу  из X в Z и затем путь из Z в Y (рекурсивное правило):
way(X,Y,[ ]):–road1(X,Y).
way(X,Y,[Z|W]):–road1(X,Z), way(Z,Y,W).
Очевиден недостаток такой записи: система, не смущаясь, будет находить маршруты, многократно проходящие через одну и ту же вершину. Чтобы избежать этого зацикливания, следует добавить проверку непринадлежности очередной вершины найденному списку вершин:
way(X,Y,[Z|W]]):- road1(X,Z), way(Z,Y,W), not(member(Z,W)).
Здесь member – знакомый предикат проверки принадлежности элемента списку.
Рекурсия неизбежно становится нехвостовой, поскольку для предиката member необходимо иметь конкретизированную величину списка W (а список этот конкретизируется только при обратном прохождении рекурсии). Но в такой рекурсии опасность зацикливания не устранена: можно без конца совершать переходы из одной вершины в другую и обратно, т.к. до проверки не принадлежности вершины маршруту вычисления просто не доходят. Очевидна необходимость хвостовой рекурсии. Можно перейти к такой рекурсии, если начать вычисления от конкретизированного списка (например, пустого) и иметь уже тем больший список, чем больше вложенность рекурсии, т.е. накапливать список в правой части правила. Но в таком случае накопленный список надо зафиксировать в базовом правиле введением дополнительного аргумента:
way(X,Y,W,W):–road1(X,Y).
way(X,Y,W,L):– road1(X,Z), not(member(Z,W)),
way(Z,Y,[Z|W],L).
Для запуска этой программы можно воспользоваться интерфейсным предикатом  go, аргументы которого содержат начальный и конечный пункты:
go(Here,There):– way(Here,There,[Here],W),
add(There,W,W1), reverse(W1,W2),  write(W2).
Здесь исходный список маршрута конкретизируется начальной вершиной. К списку найденного маршрута добавляется конечный пункт (предикат add). Предикат  reverse  выполняет инверсию этого списка. Клозы этих последних предикатов было записано ранее.
Для нахождения пути из одного заданного города в другой следует при запуске цели конкретизировать переменные Here и There. Если требуется найти путь для двух конкретных городов, проще всего ввести значения переменных стандартным предикатом Readln. В некоторых задачах необходимо организовать перебор в пространстве вершин. Наиболее корректное решение в этом случае – получить список всех вершин, а затем последовательно конкретизировать переменные вершинами из этого списка, например, с помощью предиката member или away. Вершины можно собрать в список с помощью стандартного предиката findall, использовав базу данных (фактов) задачи (см. раздел «Стандартные предикаты»).

Упражнения

1. Для улучшения алгоритма поиска в глубину можно добавить еще одно усовершенствование, а именно, ввести ограничение на глубину поиска. Программная реализация этого ограничения сводится к уменьшению на единицу величины предела глубины при каждом рекурсивном обращении и проверке, чтобы этот предел не стал отрицательным. Напишите процедуру поиска в глубину с ограничением глубины.

3.6.0 Использование структур

Одна из важных проблем при  программировании задач искусственного интеллекта состоит в выборе адекватного представления решаемой задачи в терминах понятий используемой предметной области. В программных средствах систем искусственного интеллекта для подобного представления информации широко используются структуры. Язык Пролог как раз рассчитан на очень сложные символьные структуры. Структуры данных в сочетании с рекурсивным механизмом их обработки являются мощным средством программирования в Прологе.
Понятие структуры в Прологе в некотором смысле аналогично записи в языке Паскаль. Они позволяют организовать различные фрагменты информации в единые логические единицы, что дает возможность использовать информацию, не думая о деталях ее действительного представления. Широкое применение структур – это также средство представления структурных объектов (баз данных) и управления ими. Использование структур также делает Пролог и естественным языком запросов к базе данных.
Структуры состоят из нескольких компонент. Например, дату можно рассматривать как структуру, состоящую из трех компонент: день, месяц, год. Для того чтобы объединить компоненты в структуру, требуется выбрать функтор, например, data. Тогда дату «20 февраля 2000 года» можно записать так:
data( 20, february, 2000 )
То есть функтор есть имя связи, в которую включены аргументы.
Все компоненты в данном примере являются константами. Компонентами структуры могут быть также переменные или другие структуры, в том числе эти же самые. Таким образом, структура относится к рекурсивному типу данных.  Структуры всегда выступают в качестве аргументов предикатов.
Ключевым моментом в использовании структур является вопрос сопоставления структур и унификации их компонент. При сопоставлении структур сначала проверяется, что функторы одинаковы. Затем сравниваются (слева направо) соответствующие аргументы обеих структур. В случае их совпадения процесс сопоставления продолжается. Если одна из сравниваемых переменных – свободная, то она связывается с соответствующим аргументом другой структуры. Если аргумент структуры является, в свою очередь, структурой, то правила сопоставления применяются рекурсивно для всех внутренних уровней.
Например, структуры data(D, M, 2003) и data(D1, may, Y1) сопоставимы. Конкретизацией, которая делает эти структуры идентичными, является следующая:

• D = D1
• M = may
• Y1 = 2003.

С другой стороны, структуры data(D, M, 2003) и data(D1, may, 2006) не сопоставимы
3.6.1. Объявление структур
Структура данных в Прологе задается на составной области определения (третий способ указания Domains). Для задания структуры выбирается ее имя, далее после знака «равно» записываются функторы-альтернативы данной структуры. Альтернативы перечисляются через точку с запятой. Структура может быть без альтернатив, т.е. иметь один функтор. Функтор может иметь аргументы – компоненты структуры, либо функтор может быть объявлен без аргументов. Компонентами структуры могут быть простые типы Пролога или другие структуры, в том числе те же самые, что порождает рекурсивные описания, которые могут описывать объекты сложных типов (деревьев).
Общая форма описания структур
Domains
region = functor1(d1,d2,...); functor2(d3,d4,...);...
где region объявляет сложную область(структуру),
functor1,functor2 – имена альтернатив составной области,
d1,d1,...,d3,d4 – один из типов Пролога, стандартный или определенный ранее в программе в Domains (указание типов может отсутствовать вместе со скобками).
Примеры описания структур:
Domains
data = dat( integer, string, integer )
object = int( integer );  str( string )
mesto = left; right .
После описания структур можно приступать к объявлению предикатов:
 Predicates
anyday( data )
state( mesto )
Далее записываем клозы объявленных предикатов:
Clauses
anyday( dat (1, may, 2003) ).
anyday( dat (15, june, 2001) ).
state( right ).
state( left ).
Определим еще одну область Domains – список структур:
Domains
objects = object *
Тогда можно объявить список, содержащий целые числа и строки:
Predicates
list( objects )
Clauses
list( [ int(25), int(33), str(asd), str(qwe), int(38) ] ).
Примеры рекурсивных описаний структур данных:
Domains
domains
treetype = tree( treetype, integer, treetype); empty
EXP =         var( STRING );
plus( EXP, EXP );
mult( EXP, EXP )
Первый тип подходит для построения двоичного дерева, узлы которого – целые числа. Второй тип – для записи математического выражения в префиксной форме, содержащего строки, знаки операций plus и mult, соответствующие сложению и умножению. Если теперь объявить предикаты
Predicates
TREE( treetype )
s_exp( EXP )
то для них можно записать клозы-факты. Пусть наше выражение «x + y * z». Префиксная форма записи:
 Clauses
s_exp( plus( var ( x ), mult ( var ( y ), var ( z )))).
Для небольшого дерева факт, задающий его, будет следующий:
Clauses
TREE( tree( tree( empty, 3, empty ), 6, tree( tree( empty, 2, empty ), 5, tree( empty, 7, empty ) ) ) ).
Эти описания мы будем использовать дальше.
Рассмотрим ряд примеров с использованием структур.

• База данных с использованием структур.

Создание конкретной структуры и соответствующих этой структуре объектов представляет собой создание еще одной базы данных. Объекты – это записи базы данных, а структура – описание формата такой записи и ее полей. Применение структур продемонстрируем на примере программы, которая представляет базу данных о семьях. Покажем, как извлекается информация из этой базы данных. Удачно выбранное представление облегчает интерпретацию извлеченной информации.
Каждая семья состоит, с точки представления ее логической структуры, из трех объектов: мужа, жены и детей. Поскольку количество детей в разных семьях может быть разным, то их целесообразно представить в виде списка, состоящего из произвольного числа элементов. Информацию о каждом члене семьи, в свою очередь, можно собрать структурой, состоящей из четырех компонент: имени, фамилии, даты рождения и работы. Информация о работе – это или указания кода работы и оклада, или "не работает".
Ясно, что для описания такой базы данных понадобится сложная область определения. Введем следующие структуры, соответствующие соответственно дате рождения члена семьи (число, месяц, год) и работе:
Domains
data = dat( integer, string, integer )
work = worker( string, integer );          
notwork
Тогда основная структура, соответствующая описанию каждого члена семьи, может выглядеть таким образом:
Domains
memfam= mem(string,string,data,work);
absent                      % Член семьи может отсутствовать
list_memfam = memfam *
Информацию о двух семьях можно занести в базу данных с помощью  следующих описаний и предложений:
Predicates
family (memfam, memfam, list_memfam)
Clauses
family(mem(jon, kelly, dat(17, may, 1950), worker(bbz, 15000)),
mem(bony, kelly, dat( 29, may, 1951), notwork)),
[mem(pat, kelly, dat(5, april, 1983), notwork),
mem(liz, kelly, dat(10, april, 1960), notwork)).
family(mem(bob, rob, dat(14, may, 1930), worker(pla, 12000)),
mem(sally, rob, dat(5, october, 1931), worker(plt, 11000)), [ ]).     % нет детей в семье
Теперь из такой базы данных уже можно извлекать информацию. Так, в запросах к базе данных можно ссылаться на всех kelly с помощью цели:
goal:  family(mem( _ , kelly, _ , _ ), _ , X ).
Данная цель вернет значение переменной – список структурированных объектов, содержащий информацию о детях семью Келли:
X = [mem(pat, kelly, dat(5, april, 1983), notwork),
mem(liz, kelly, dat(10, april, 1960), notwork)).
Символы подчеркивания в записи цели обозначают различные анонимные переменные, значения которых нас не интересуют.
Можно найти все семьи с тремя детьми при помощи выражения:
goal:   family( X, _ , [ _ , _ , _ ] ).
Здесь переменная X будет конкретизирована структурой, представляющей первый аргумент предиката family.
Чтобы найти имена и фамилии всех женщин, имеющих, по крайней мере, трех детей, можно задать вопрос:
goal:   family( _ , mem( Name, Fam, _ , _ ), [ _ , _ , _ | _ ] ).
Главным моментом в этих примерах является то, что указывать интересующие нас объекты можно не только по их содержимому, но и по их структуре, т.е. иметь результат в виде целой структуры или в виде отдельных элементов структур.
Можно также создать набор процедур, который делал бы взаимодействие с базой данных более удобным. Такие процедуры являлись бы частью пользовательского интерфейса. Вот некоторые из них:
husband(X) :– family( X, _ , _ ).                              % X – муж
vife(X) :– family( _ , X , _ ).                                    % X – жена
child(X) :– family( _ , _ , Children ),          % X – ребенок
member( X , Children ).
exist(X) :– husband( X ); vife( X ); child( X ).                      % X – любой член семьи
Этими процедурами можно воспользоваться, например, в следующих запросах к базе данных:
1) найти имена и фамилии всех людей из базы данных:
Goal: exist( mem( Nam, Fam, _ , _ )).
2) Найти всех работающих жен:
Goal: vife(mem( Nam, Fam, _ ,worker( _ , _ ))).
Другой способ извлечения информации из структурированной базы данных – через так называемый предикат-селектор. Селектор позволяет извлечь Общий вид такого предиката-селектора:
селектор(Структурный объект, Выбранная компонента).
Селектор позволяет извлечь отдельные компоненты структуры. Например, если хотим извлечь величину дохода отдельного члена семьи, следует записать селектор:
dohod(mem( _ , _ , _ , worker( _ , D)), D ).                         % D – доход работающего
dohod(mem( _ , _ , _ , notwork), 0 ).                                  % 0 – доход неработающего
Ясно, что селектор требует конкретизированный первый аргумент, поэтому селектор всегда используется в правой части правила или в цели, предварительно конкретизирующей структуру. Тогда, чтобы найти людей, чей доход меньше чем 8000, можно записать цель:
Goal: exist(Man), dohod(Man, D), D < 8000.
Видно, что при использовании селектора структурный объект (переменная Man) задан как единое целое. Пролог прекрасно справляется с «расщеплением» структуры и извлечением из нее отдельных единиц информации. Использование отношений-селекторов позволяет забыть о  деталях представления информации и облегчает написание и последующую модификацию программ.
3.6.2. Задача "Ханойская башня". Имеется три стержня А,В,С. На стержне А лежит N дисков пирамидой, сужающейся кверху. Надо переместить диски со стержня А на стержень C, используя промежуточный стержень B  и соблюдая законы:
1) диски можно перемещать с одного стержня на другой по одному;
2) нельзя класть больший диск на меньший;
3) при переносе дисков с одного стержня на другой можно использовать промежуточный третий стержень, на котором диски должны находиться тоже только в виде пирамиды.
Если в программе использовать рекурсивную процедуру, то программа становится удивительно маленькой: два рекурсивных вызова процедуры и оператор вывода результатов перемещения дисков.
Собственно "перемещению" диска соответствует оператор вывода, указывающий, с какого стержня на какой переместить диск. Основным рабочим предикатом является рекурсивный предикат move. Базовое правило этой рекурсии: если диск один, то переместить его с левого стержня на правый. Иначе, переместить N-1 диск с левого диска на средний промежуточный, переместить один диск с левого стержня на правый и затем переместить N-1 диск со среднего стержня на правый, используя левый стержень как промежуточный.
Domains
loc = right; middle; left
predicates
hanoi(integer)
move(integer, loc, loc, loc)
inform(loc, loc)
clauses
hanoi(N) :– move(N, left, middle, right).                       % Запуск программы
move(1, A, _, C) :– inform(A, C), !.                                % Переместить один диск
move(N, A, B, C) :–                                                       % Переместить  N  дисков
N1=N-1, move(N1, A, C, B),
inform(A, C), move(N1, B, A, C).
inform(Loc1, Loc2) :– write("\nMove a disk from ", Loc1, " to ", Loc2).
Goal hanoi(10).                                                                 % Перемещаем 10 дисков
3.6.3. Задача о перевозке через реку волка, козы и капусты. Предполагается, что вместе с человеком в лодке помещается только один объект и что человеку приходится охранять козу от волка и капусту от козы. Типичная задача, описываемая пространством состояний. Пространство состояний - это граф, вершины которого соответствуют ситуациям, встречающимся в задаче, а решение задачи сводится к поиску пути в этом графе между заданной начальной ситуацией (стартовой вершиной) и некоторой конечной ситуацией, называемой целевой вершиной.
Пространство состояний можно указывать явно в виде набора двухаргументных отношений. Такое отношение истинно, если существует разрешенный ход. Однако этот принцип оказывается непрактичным и нереальным, когда пространство состояний достаточно велико. Поэтому отношение следования обычно определяется неявно при помощи правил вычисления вершин-преемников некоторой заданной вершины. Использование структур дает возможность  программировать пространство состояний, взамен полного перебора их описаний.
Каждый из четырех объектов (фермер, волк, коза и капуста) может находиться  в одном из двух состояний LOC: east  или  west, в зависимости от того, на каком берегу (восточном или западном) они находятся. Общее состояние всех субъектов описывается структурой STATE. Понятно, что если в начальный момент все объекты находятся в состоянии  east, то программа должна перевести их в состояние  west, избегая запрещенных состояний. К запрещенным состояниям относятся следующие: фермер в одном состоянии, например  east, а волк и коза – в состоянии  west, т.е. при отсутствии фермера волк съест козу; к другим запрещенным состоянием относятся присутствие вместе козы и капусты в отсутствие фермера. Последовательность допустимых переходов структур STATE даст искомое решение.
DOMAINS
LOC   = east ; west
STATE = state(LOC,LOC,LOC,LOC)
PATH  = STATE*
PREDICATES
go(STATE,STATE)                                 %  запуск программы
path(STATE,STATE,PATH,PATH)           %  основной рабочий предикат
move(STATE,STATE)                            %  одна перевозка
opposite(LOC,LOC)                               %  переход в противоположное состояние
unsafe(STATE)                                      %  запрещенное состояние
member(STATE,PATH)              %  проверка принадлежности
write_path(PATH)                                  %  оформление вывода

GOAL
makewindow(4, 7, 0, "", 0, 0, 24, 80),
go(state(east, east, east, east), state(west, west, west, west)),
write("solved press any key to continue"),
readchar( _ ),
exit.
CLAUSES
go(S,G) :-  path( S, G, [ S ], L ),
nl, write("A solution is:"), nl,
write_path( L ),
fail.
go( _ , _ ).
path( S, G, L, L1 ) :-  move( S, S1 ),
not( unsafe( S1 ) ),
not( member( S1, L ) ),
path( S1, G, [ S1 | L ], L1 ), !.
path( G, G, T, T ):-  !.                             % Базовое правило, последний
% аргумент фиксирует результат

move(state( X, X, G, C ), state( Y, Y, G, C )):-opposite( X, Y ). % фермер + волк
move(state( X, W, X, C ), state( Y, W, Y, C )):-opposite( X, Y ).  % фермер + коза
move(state( X, W, G, X), state( Y, W, G, Y )):-opposite( X, Y ) .  % фермер + капуста
move(state( X, W, G, C ), state( Y, W, G, C )):-opposite( X, Y ).  % только фермер
opposite( east, west ).
opposite( west, east ):- !.
unsafe( state( F, X, X, _ ) ):- opposite( F, X ).     /* волк съест козу              */
unsafe( state( F, _ , X, X ) ):- opposite( F, X ).    /* коза съест капусту        */
member( X , [ X | _ ] ).
member( X, [ _ | L ] ):-member( X, L ).

3.6.4. Планирование воздушного путешествия (143 Бр)
В этом примере мы разберем программу, которая даст советы по планированию воздушного путешествия. По сравнению с программой поиска пути на графе, которая позволяет найти путь между двумя годами, задача усложняется тем, что время вылета из каждого города фиксировано и, кроме того, нужно оставить достаточно времени на пересадку между двумя перелетами. Предполагается, что все перелеты совершаются в один и тот же день.
Вспомним представление пространства состояний в задаче поиска пути на графе. Оно имело простую структуру, содержащую информацию о попарно соединенных вершинах графа. Основное отличие базы данных для этой программы то, что она должна содержать достаточно полную информацию для реализации наших целей. Поэтому не обойтись без структурированных данных. База данных будет представлена фактами, содержащими информацию о рейсах, собранных в расписании:
raspisanie(T1, T2, Spis_reis),
где T1, T2 – названия двух городов,
Spis_reis – это список, состоящий из структурированных объектов, содержащих информацию об отдельных рейсах, выполняемых между городами T1 и T2. Один конкретный рейс, например, может быть такой структурой:
reis(N_reisa, Time_otprav, Time_prib, Spis_dn)
Здесь N_reisa – номер рейса,
Time_otprav – время отправления,
Time_prib – время прибытия рейса,
Spis_dn – список дней вылета, это либо список дней недели, либо терм «ежедневно».
Время представлено также в виде структурированных объектов, состоящих из двух компонент: часов и минут:
time( 9, 40 ).
Один из фактов базы данных может быть, например, таким:
 raspisanie (“Moskva”, “Piter”, [             reis( 1416, time( 9, 0 ), time( 10, 50 ), [pnd, ptn, vskr]),
                                                                        reis( 2010, time( 12, 30 ), time( 14, 10 ), [vtr, cht, sbt]),
                                                                        reis( 2215, time( 17, 10 ), time( 18, 50 ), everyday) ] ).
Таким образом, база данных содержит полную информацию, необходимую для целей нашей задачи. На этом описание фактов можно считать законченным и можно переходить к правилам.
Основным предикатом, соответствующим переводу системы в новое состояние, т.е. прямому перелету из одного города в другой, будет предикат reis:
reis(T1, T2, D, N_reisa, Time_otpr, Time_prib):-
raspisanie(T1, T2, Spis_reis),
member( reis(N_reisa, Time_otprav, Time_prib, Spis_dn), Spis_reis),
member(D, Spis_dn).
Для конкретных городов T1 и T2 обращение к факту базы данных raspisanie даст список рейсов Spis_reis для этих городов, а первый предикат принадлежности получит конкретный рейс из этого списка. В результате будет конкретизированы: номер рейса, время отправления, время прибытия и список дней вылета Spis_dn, а с  помощью второго предиката member будет конкретизирован день вылета D.
Далее задача нахождения маршрута сводится к классической задаче поиска пути на графе с дополнительными переменными. Базовое правило:
way( T1, T2, D, [ perelet( N_reisa, T1, T2, Time_otpr ) ] ):-
reis(T1, T2, D, N_reisa, Time_otpr, Time_prib).
Правило с рекурсией:
way( T1, T2, D, [ perelet(N_reisa, T1, T3,Time_otpr ) | W ] ):-
way( T3, T2, D,  W ),
reis( T1, T3, D, N_reisa, Time_otpr1, Time_prib1 ),
t_otprav( W, Time_otpr2 ),
peresadka( Time_prib1, Time_otpr2 ).
Здесь t_otprav и peresadka – предикаты-селекторы, оперирующие с отдельными компонентами структуры:
t_otprav( [ perelet( N_reisa, T1, T3,Time_otpr) | _ ], Time_otpr ),
peresadka( time( C1, M1 ), time( C2, M2 )):-  (60*( C2-C1 ) + ( M2-M1 )) >= 40.
Предикат принадлежности member должен быть описан дважды в секции predicates, поскольку его аргументами в разных случаях являются структуры и списки структур разного типа.
3.6.5. Реализация Планировщика в терминах структур
Здесь мы рассмотрим реализацию планировщика с использованием абстрактных типов данных, описываемых с помощью структур Пролога.

                                                                 а)                                                           б)
Рис. Начальное (а) и конечное (б) состояние мира блоков
Эту задачу можно представить как задачу поиска в пространстве состояний. Для этого нужно учесть все возможные перемещения, доступные в каждый момент решения задачи. Состояние мира можно представить с помощью списка блоков, причем последовательность описания произвольна, т.е. список представляет собой множество. Над списками удобно выполнять такие операции как добавление, удаление, пересечение, разность, равенство.
Состояние мира блоков, включая начальное и целевое, можно представить в виде списков таким образом:
Start = [ ontable(a), ontable(b), ontable(c) ],
Stop = [ on(c, b), on(b, a) ].
Для этого укажем следующую область определения:
Domains
state = ontable( char );
on( char, char );
clear( char );
hand
states = state*
Правила изменения состояния в процессе поиска – это продукционные правила. Определим их на языке Пролог как правила move. Рекурсивный предикат path обеспечит механизм поиска в продукционной системе.
В хорновской дизъюнктивной форме шаблоны текущего и последующего состояний должны располагаться в голове дизъюнктивного выражения, т.е. слева от оператора “:–“. Они являются аргументами предиката  move. Условия,  которым должно удовлетворять продукционное правило для получения следующего состояния, размещаются справа от оператора “:– “.
Сначала определим правило move для помещения блока X на блок Y. В отсутствие прочих ограничений (например, на размеры блока) это правило применимо, если блок Y свободен:
move(X, Y):- clear(Y).
В целом задача похожа на пример 3.6.2 о перевозке через реку и сводится к поиску пути на графе: начальное и конечное состояния описаны в терминах структур, поиск в пространстве состояний сводится к нахождению последовательности действий и накоплению их в список с исключением циклов.
3.6.6. Задача «Зебра»
Эта задача известна как «проблема пяти домов». В пяти соседних домах, окрашенных в разные цвета, живут пять человек различных национальностей. У каждого из них есть свое любимое домашнее животное, своя манера курить и свой любимый напиток. Спрашивается, кому принадлежит зебра.
Задача интересна тем, что пространство состояний не имеет описания в явном виде реляционной базы данных. Все отношения «после» генерируются.
Программа реализует алгоритм, имеющий название «порождение и проверка». Это один из методов работы с большими пространствами состояний. Алгоритм состоит из двух основных шагов:

• генерация нового состояния;
• проверка достижения конечного состояния.

Каждым новым состоянием является перестановка элементов списков, представляющих элементы исходных условий задачи. Конечным состоянием является принадлежности целевого состояния сгенерированному списку; в нашем примере конечным состоянием является наличие элемента «zebra» в списке домашних любимцев.
Кандидатами решения является распределение пяти цветов домов, пяти напитков, пяти национальностей жильцов, пяти видов сигарет и пяти видов домашних любимцев по соответствующим спискам.
Основными рабочими предикатами, реализующими генерацию состояний и перебор, являются constraints и candidate. Первый из них генерирует список c пока еще анонимными переменными в качестве второго аргумента (номера дома). Например, списки расцветок домов и национальностей выглядят следующим образом:
[h(“red”, _ ), h(“yellow”, _ ), h(“blue”, _ ), h(“green”, _ ), h(“ivory”, _ )]
[h(“englishman”, _ ), h(“spaniard”, _ ), h(“norwegian”, _ ), h(“ukrainian”, _ ), h(“japanese”, _ ) ]
Предикат candidate путем перестановок пытается конкретизировать второй аргумент:
[h(“red”, 3), h(“yellow”, 1), h(“blue”, 2), h(“green”, 5), h(“ivory”, 4)]
[h(“englishman”, 3), h(“spaniard”, 4), h(“norwegian”, 1), h(“ukrainian”, 2), h(“japanese”, 5) ]
Полный листинг программы приведен ниже.
DOMAINS
/* Элемент структуры идентифицируется строкой и номером        */
HOUSE = h(SYMBOL, NR)                      
HLIST  =  HOUSE*   /* Список структур                                          */            
NR = INTEGER                                          /* Номер дома                                                     */
NRLIST = NR*
CHARLIST = CHAR*
CHARLISTS = CHARLIST*

PREDICATES
solve
outlist(NR, HLIST)
candidate(HLIST, HLIST, HLIST, HLIST, HLIST)
perm(HLIST)
constraints(HLIST, HLIST, HLIST, HLIST, HLIST)
permutation(NRLIST, NRLIST)
delete(NR,NRLIST, NRLIST)
member(HOUSE, HLIST)
next(NR,NR)
lleft(NR,NR)

GOAL
makewindow(1,7,0,"",0,0,25,80),
solve.                                                       /* Начало вычислений */

CLAUSES
solve( ) :-
constraints(Colours, Drinks, Nationalities, Cigarettes, Pets), % Проверка условий
candidate(Colours, Drinks, Nationalities, Cigarettes, Pets), % Задает перестановку
member( h(zebra, _ ), Pets ),       % Проверка принадлежности зебры списку любимцев
outlist(1, Colours),
outlist(2, Drinks),
outlist(3, Nationalities),
outlist(4, Cigarettes),
outlist(5, Pets).

outlist( _ , [ ]) :- !.
outlist(Line, [ h(String, House)| T ] ) :-
sign(House, Line, String), outlist(Line, T).

candidate(L1, L2, L3, L4, L5) :-
perm(L1),
perm(L2),
perm(L3),
perm(L4),
perm(L5).

perm( [h( _ , A),h( _ , B),h( _ , C),h( _ , D),h( _ , E ) ] ) :-
permutation( [ A, B, C, D, E ], [ 1, 2, 3, 4, 5 ] ).

constraints(C, D, N, S, P)  :-
/* Англичанин живет в красном доме */
member(h(englishman,H1), N),
member(h(red,H1), C),
/* Испанец владеет собакой */
member(h(spaniard,H2), N),
member(h(dog,H2), P),
/* Норвежец живет в первом доме слева */
member(h(norwegian,1), N),
/* «Кулз» курят в желтом доме */
member(h(kools,H3), S),
member(h(yellow,H3), C),
/* Человек, который курит «честерфилдз» */
/* живет в соседнем доме с мужчиной, который держит лису */
member(h(chesterfields,H4), S),
next(H4, H5),
member(h(fox,H5), P),
/* Норвежец живет в соседнем с голубым домом */
member(h(norwegian,H6), N),
next(H6, H7),
member(h(blue,H7), C),
/* «Винстон» курит хозяин улиток */
member(h(winston,H8), S),
member(h(snails,H8), P),
/* «Лаки страйк» курит любитель апельсинового сока */
member(h(lucky_strike,H9), S),
member(h(orange_juice,H9), D),
/* Украинец пьет чай */
member(h(ukrainian,H10), N),
member(h(tea,H10), D),
/* Японец курит «парламентс» */
member(h(japanese,H11), N),
member(h(parliaments,H11), S),
/* «Кулз» курят в доме, соседнем с домом, где держат лошадь */
member(h(kools,H12), S),
next(H12, H13),
member(h(horse,H13), P),
/* Кофе пьют в зеленом доме */
member(h(coffee,H14), D),
member(h(green,H14), C),
/* Зеленый дом справа от бежевого дома */
member(h(green,H15), C),
lleft(H16, H15),
member(h(ivory,H16), C),
/* Молоко пьют в доме, находящемся посередине, т.е. на третьем месте */
member(h(milk,3), D).

/* Инструментарий */

permutation([ ],[ ]).
permutation([A|X],Y) :- delete(A,Y,Y1), permutation(X,Y1).
delete(A,[A|X],X).
delete(A,[B|X],[B|Y]) :- delete(A,X,Y).
member(A,[A| _ ]) :- !.
member(A,[ _ |X]) :- member(A,X).
next(X,Y) :- lleft(X,Y).
next(X,Y) :- lleft(Y,X).
lleft(1,2).
lleft(2,3).
lleft(3,4).
lleft(4,5).
3. Рекурсивное описание данных. В Domains описывается древовидная рекурсивная структура, узлы которой - данные типа string либо empty. Данная программа представляет собой пример двоичной классификации растений, при этом очередной узел дерева соответствует задаваемому вопросу, левая ветвь - ответу "да", правая - "нет":

Рис.Дереводвоичнойклассификации

domains
treetype = tree(string, treetype, treetype); empty
predicates
TREE( treetype )
gotree( treetype )
gotreeA( char, treetype )
clauses
TREE(         tree("стебель древесный", tree("растение стоит прямо",
tree("растение имеет один стебель",
tree("дерево", empty, empty ), tree( "кустарник", empty, empty )),
tree("лиановые", empty, empty )), tree( "травянистые", empty, empty ))).
gotree( tree( X, empty, empty )) :-write( "тип растения - ", X ).
gotree( tree( X, LT, RT )):- write( X, " ?" ), nl, readchar( A ),
gotreeA( A, tree( X, LT, RT )).
gotreeA( 'y', tree( _ , LT, _ )) :- gotree( LT ).
gotreeA( 'n', tree( _ , _ , RT )) :-gotree( RT ).
goal
makewindow( 1 , 2, 3, "", 0, 0, 25, 80 ),
TREE( D ),
gotree( D ).

Упражнения

1. Допишите программу реализации планировщика в терминах структур и представления «мира блоков» в виде списка. Добавьте предикаты манипулирования в мире блоков с помощью манипулятора

3.7. Динамическая база данных

Пролог поддерживает реляционную базу данных. Предикаты базы данных нужно объявлять в отдельном разделе Database. Программная секция Database должна предшествовать объявлению предикатов Predicates. Объявление предикатов базы данных аналогично их описанию в секции Predicates.
Динамическая база данных – раздел программы, в котором факты могут добавляться или загружаться из файла на диске во время выполнения программы или удаляться из нее. Факты, описывающие предикат базы данных, могут также обрабатываться как обыкновенные предикаты Пролога.
Встроенные предикаты  asserta и assertz позволяют программисту добавлять новые утверждения в базу данных Пролога. Поскольку Пролог декларирует идентичность программ и данных, то риск изменения программы является главной причиной того, что надо проявлять известную осторожность при использовании предикатов assert и retract Этот риск минимизируется четким логическим разделением информации, связанной с данной задачей. Информация может быть постоянная и переменная. Постоянная информация – это программная часть, например, база знаний задачи, а переменной информацией могут быть данные, поступающие в ходе диалога  Изменениям подвергаются только переменные данные.
Базу данных Пролога можно трактовать как некую глобальную переменную. Такая трактовка очень удобна: любая процедура может записывать в нее свой результат, который будет доступен любой другой процедуре, какая бы дистанция между ними ни была при их последовательных динамических вызовах. Передача аргументов через динамическую базу данных в ряде случаев оказывается более предпочтительной, чем передача их через параметры предикатов.

3.7.1. Использование стандартных предикатов динамической базы данных

Для работы с базой данных используют стандартные предикаты asseta, assertz, retractall, consult, save и др. (см. раздел  "Стандартные предикаты"). Также нужно иметь представление о структуре памяти системы Пролога. Исходная программа на Прологе хранится в области SOURSE, в то время как для размещения фактов динамической базы данных отведена область HEAP. Поэтому на экране нельзя видеть информацию, записанную в базу данных. Однако ее можно просмотреть как текстовый файл, если сохранить его в каталоге под своим именем.
23. Пример работы с динамической базой данных.
Domains
         list=integer*
Database – db1                        % База данных с именем db1
         fact1(integer,string,list)
Database – db2                         % База данных с именем db2        
         fact2(integer,string)
Clauses 
                    /*Факты базы данных описаны как обыкновенные предикаты*/
         fact1(1,f1,[1,2,3]).
fact1(2,f2,[1,3]).
         fact1(3,f3,[2,2,1]).
         fact2(1,],"one").
         fact2(1,"one one"]).
         fact2(2,"two").
Тогда цель:
Goal   fact1(X,Y,Z)
ответит:
         X=1  Y=f1  Z=[1,2,3])
         X=2  Y=f2  Z=[1,3]).
         X=3  Y=f3  Z=[2,2,1]).
            3 solutions
Goal   rettactall(fact1(X,Y,[_,2|Z]))      % удалить факты по образцу
         X=1  Y=f1  Z=3
         X=3  Y=f3  Z=1
Goal   retractall(fact1(X,Y,Z))
         X=2  Y=f2  z=[1,3]
Goal   retractall(db2)                  % удалить поименованную базу данных
              Yes .

24. Создание базы данных "Таблица умножения".
Domains
list = integer *
Database
mult( integer, integer, integer )   % Непоименованная база данных
Predicates
tabl
numlist( list )
member( integer, list )
Clauses
numlist( [ 1, 2, 3, 4, 5, 6, 7, 8, 9 ] ).
tabl:- numlist( L ),
member( X, L ), member( Y , L ),    %  X  и Y - целые числа из списка L
Z = X * Y,
assertz( mult( X, Y, Z )), fail.          % Факт mult добавляется в динамическую базу данных
tabl.
member( X , [ X | _ ] ).
member( X, [ _ | T ] ):- member( X, T ).
Зададим в диалоговом окне следующую цель:
     Goal   tabl,                            %  Создание базы данных
               mult( 2, 5, X ).                %  Обращение к базе данных
Система ответит:
          X = 10  Yes.
     Goal mult( 10, 10, X ).
     Система ответит
  No ,
поскольку в базе данных нет такого факта. Допишем в секцию Clauses пару фактов:
Clauses
         mult( 10, 10, 100 ).
         mult( 9, 10, 90 ).
Тогда система будет находить эти факты, но не в области динамической базы данных, а фактов программной секции Clauses.
Следующая цель позволит сохранить базу данных на диске под выбранным именем:
     Goal   tabl, 
         save( “mytabl.db” ).                         %  Сохранение базы данных на диске
Теперь клозы предиката  mult будут сохранены как обычный файл (можете просмотреть его в своем рабочем каталоге), и, следовательно, могут быть загружены в динамическую память при следующем сеансе работы. Для этого следует запустить цель:
Goal    
         consult( “mytabl.db”).                         %  Загрузка базы данных в динамическую память
Таким образом, динамическая база данных Пролога обеспечивает не только удобный механизм работы с динамической памятью, но также выступает в роли файловой системы, реализуя высокоуровневые операции доступа к внешним файлам. Следует отметить, что в Прологе также имеются низкоуровневые операции доступа к файлам, аналогичные имеющимся в других языках программирования (C, Pascal, см. «Стандартные предикаты»).
Пример. Манипулирование в мире блоков. Состояние мира можно сохранять в динамической БД в виде фактов. Чтобы добавить факты, зададим цель:
Goal assert( ontable( a ) ), assert( ontable( b ) ), assert( ontable( c ) ).
Пусть имеем некоторые предикаты манипулирования:
clear( X ) :- not( on( _ , X ).
pick_up( X, Y ) :- clear( Y ),
                     retract( ontable( X ) ),
                      assert( on( X, Y ) ).
Чтобы поместить b на c, зададим вторую цель:
Goal pick_up( b, c ).  
В базе данных удалится факт ontable(b) и запишется факт on(b,c).

Упражнения

1. Определите, будет ли каждая из следующих пар структур сопоставимой. Если пара сопоставима, найдите значения, которыми будут замещаться переменные в структурах.
а) data(day(sunday), number(21), month(M), year(1995))  и
data(Day, Number, Month, Year)
б) book(title(“Ферма животных”), name(“Дж. Оруэлл”))  и
book(title(T), Name)
в) animal(cat(“лапы”), dog(“клыки”)) и
animal(Animal, Animal)

3.8. Средства управления

Управление в Прологе осуществляется с помощью предикатов, позволяющих изменять выполнение программы. К настоящему моменту мы познакомились с некоторыми средствами управления в Пролог-программе. К ним относятся:

• fail – цель, которая всегда терпит неудачу;
• true – цель, которая всегда успешна;
• not(P) – отрицание, которое всегда ведет себя в точном соответствии со следующим определением: 

not(P) :- P, !, fail; true.

• repeat – цель, которая всегда успешна. Она недетерминирована, поэтому, когда до нее доходит перебор, она порождает новую ветвь вычислений.

К другим средствам управления, позволяющим существенно влиять на вычислительный процесс, является использование некоторых стандартных предикатов.
1. Отсечение, обозначаемое восклицательным знаком («!»). Если в теле дизъюнкта встречается отсечение, то все утверждения между головой дизъюнкта и знаком «!» не могут пересогласовываться (переконкретизироваться). Перебор возможен только между головой дизъюнкта и знаком отсечения.
Пример. Пусть имеются следующие описания.
a(x):-b(X),!,c(X).
a(x):-d(X).
b(e).
b(f).
c(e).
c(f).
d(g).
Если бы не было знака отсечения, на запрос a(Z) было бы выдано три ответа:
Z=e,
Z=f,
Z=g.
Из-за отсечения программа даст один ответ Z=e. Она не будет обращаться к разветвлениям, возможным после отсечения. Второе правило a(x) также игнорируется.
Отсечение применяется в следующих основных случаях.
1) Прекращение бессмысленного перебора (бэктрекинга). Рассмотрим знакомый предикат принадлежности элемента списку. Первый клоз этого предиката можно записать в виде правила:
member(X, [X| _ ]) :- ! .
member(X, [ _ | T ]):– member(X,T).
Как только будет найдено первое вхождение X в список, работа предиката прекращается, т.е. теперь процедура дает единственное решение. Мы повысили эффективность программы, оставив при этом ее декларативный смысл без изменения. Такое отсечение, не меняющее декларативный смысл программы, называется «зеленым отсечением22»

• Отсечение как неуспех. Рассмотрим фразу: «Мэри любит всех животных, кроме змей». Как выразить это на Прологе?  Первую часть этого утверждения выразить легко: «Мэри любит всякого Х, если Х – животное»:

likes(“Мэри”, X) :- animal (X).
Но нужно исключить змей. На Прологе сказать, что  что-либо не есть истина можно с помощью встроенного предиката fail (неуспех). Записанное далее отсечение предотвратит дальнейший перебор. Правило со змеей как исключительный случай, следует рассмотреть в первую очередь:
likes(“Мэри”, X) :- animal (X), X = “змея”, ! , fail.
likes(“Мэри”, X) :- animal (X).
Здесь первое правило позаботится о змеях: если Х – змея, то отсечение предотвратит перебор, исключая таким образом второе правило из рассмотрения, а fail вызовет неуспех. Отсечение в этом примере меняет декларативный смысл программы и называется «красным отсечением»0,.  
2. Собрать все решения в список. Эту работу выполняет высокоуровневый предикат findall:
findall( Variable, Atom, ListVariable )
В списке ListVariable возвращаются все решения для переменной Variable предиката Atom.
При помощи механизма перебора можно пучить все решения, удовлетворяющие некоторой цели. Однако всякий раз, когда порождается новое решение, предыдущее пропадает и с этого момента становится недоступным. Если хотим получить доступ ко всем порожденным объектам сразу, можно собрать их в список, что обеспечивает встроенный предикат  findall. Например, у нас есть предикаты-факты, представляющие некоторые результаты:
result( “Иванов”, 370).
result( “Петров”, 230).
result( “Иванов”, 160).
Чтобы получить список результатов, например, Иванова, зададим цель:
Goal findall(R, result( “Иванов”, R), List), write(List).
Полученный результат:
List=[370,160].
Получить список всех фамилий можно целью:
Goal findall(Fam, result( Fam, _ ), List), write(List).
Список всех фамилий:
List=[“Иванов”, “Петров”, “Иванов” ].
В список можно собирать практически объекты любого типа, включая сами же списки и другие структурные объекты Пролога. В программе только требуется объявить необходимую область определения Domains. Например, имеем предикаты:
result( [10, 20, 30]).
result( [40, 50]).
Укажем область определения для предиката findall:
Domains
list = integer*
Llist = list*
и можно задавать цель
Goal findall(L, result( L ), L1), write(L1).
В результате получим список списков
L1=[ [10, 20, 30], [40, 50] ].
Предикат  findall является процедурой очень высокого уровня, поскольку выполняет много промежуточной работы. Его также можно использовать для запуска других предикатов. Допустим, предикат go(town1,town2,L) находит путь из одного города в другой. Чтобы найти все пути, ведущие из города town1 в town2, запустим цель:
Goal findall(L, go( town1, town2, L ), L1), write(L1).

3.9. Представление множеств двоичными деревьями

Теперь, когда мы рассмотрели основные вычислительные механизмы Пролога, можно приступить к наиболее интересным реализациям программ. Первыми рассмотрим программы представление множеств двоичными деревьями
Списки часто используют для представления множеств. Такое использование списков имеет тот недостаток, что проверка принадлежности элемента множеству оказывается довольно неэффективной. Для более эффективной реализации отношения принадлежности применяют различные древовидные структуры, в частности, двоичные деревья.
Существует много способов представления двоичных деревьев на Прологе. Наиболее привычный способ: выбрать специальный символ для обозначения пустого дерева и функтор для построения непустого дерева из трех компонент (корня и двух поддеревьев). Сделаем следующий выбор.
Пусть атом nil представляет пустое дерево. В качестве функтора примем  tr, так что дерево с корнем  X, левым поддеревом L и правым поддеревом R будет иметь вид терма tr(L,X,R).
С двоичным деревом легче работать, если оно упорядочено. Такое дерево называется двоичным справочником. Чтобы можно было построить такое дерево, определим отношение "добавить лист" (adlist). Правила добавления элементов на уровне листьев таковы:
- результат добавления элемента X к пустому дереву есть дерево   tr(nil,X,nil).
- если X совпадает с корнем дерева D, то лист не добавляется.
- если корень дерева D больше, чем X, то X вносится в левое поддерево дерева D;
- если корень меньше чем X, то X вносится в правое поддерево.
adlist( nil, X, tr( nil, X, nil )).
adlist(tr( L, X, R ), X, tr( L, X, R )).
adlist(tr( L, K, R ), X, tr( L1, K, R )):-
X < K, adlist( L, X, L1 ).
adlist(tr( L, K, R ), X, tr( L, K, R1 )):-
X > K, adlist( R, X, R1 ).
Для построения дерева введем цикл while. В результате работы двоичное дерево будет записано в базу данных.
domains
tre = tr( tre, integer, tre); nil
database
ntree( tre )
predicates
tree( tre )
adlist( tre, integer, tre )
while( integer, tre )
clauses
tree(tr(tr( nil, 6, nil ), 8,
tr(tr( nil, 10, nil ), 9, nil ))).            % Пример двоичного дерева
adlist( nil, X, tr( nil, X, nil )).
adlist(tr( L, X, R ), X, tr( L, X, R )).
adlist(tr( L, K, R ), X, tr( L1, K, R)):-
X < K, adlist( L, X, L1 ).
adlist(tr( L, K, R ), X,tr( L, K, R1 )):-
X > K, adlist( R, X, R1 ).
while( 999, D ):- asserta( ntree( D )), !.
while( X, D):- adlist( D, X, D1 ), readint( X1 ), while( X1, D1 ).
Goal
while( 7, nil ), ntree( X ).
Пользователю будет несложно  построить отношение принадлежности   вершины X  дереву T,  которое истинно, если X есть одна из вершин дерева T.

3.9. Программы классификации

Эти программы классификации представляют собой по сути прототип некоторой экспертной системы, поскольку реализуют собой основной блок экспертной системы – вывод на знаниях, которые представлены в виде совокупности фактов и правил.
Основой задач классификации является так называемое решающее дерево. Информация представлена в виде иерархической структуры классификационных правил типа «Если – То» Здесь мы рассмотрим вопросно-ответную систему, которая является примером небольшой экспертной системы в том смысле, что программа варьирует процесс опроса в зависимости от обстоятельств; более того, она может задавать минимально необходимое число вопросов.
Основой базы данных такой программы является дерево решений некоторой предметной области. В нашем случае таким деревом будет система классификации животных. Все животные делятся на млекопитающих, птиц и рыб. Среди млекопитающих могут быть хищники и копытные. К хищникам, в частности, относятся тигр и гепард.

Рис. Классификационное дерево

Преобразовать классификационное дерево в набор правил можно, если проследить все возможные пути, ведущие к логическому выводу. Для нашего классификационного дерева не хватает существенных элементов: параметров, или условий классификации, например, при каких условиях млекопитающее является хищником. Другими словами, дугам дерева требуется приписать условия, обеспечивающие спуск от одного уровня дерева к другому.
С учетом сказанного, наше дерево может быть описано набором продукционных правил следующим образом (на примере одного пути дерева):
Если животное имеет шерсть
И кормит детенышей молоком
То животное является млекопитающим
Таким же образом можно перейти к следующему уровню дерева от млекопитающего к хищнику:
Если млекопитающее имеет острые зубы
И имеет когти
И имеет глаза, направленные вперед
То млекопитающее является хищником
И, наконец, переход к нижнему уровню:
Если хищник имеет рыжий цвет
И имеет черные полосы
То хищник является тигром
Программа классификации может быть реализована с прямой или обратной цепочкой рассуждений. Обратная цепочка рассуждений может быть успешно применена к задачам, в которых имеется всего несколько решений при наличии больших объемов входной информации. В этом случае целесообразно выбрать одно из возможных решений, а затем собрать все свидетельства, которые могут его подтвердить или опровергнуть.

3.9.1. Программа классификации с обратной цепочкой рассуждений

Первой приведем пример версии программы с обратной цепочкой рассуждений, т.к. она ближе к встроенному в Пролог механизму вывода, и, следовательно, реализуется достаточно прямолинейно.
Обратная цепочка рассуждений предполагает продвижение от цели, в нашем случае от распознаваемого животного. Структура версии с обратной цепочкой рассуждений проектируется введением группы правил высокого уровня, т.е. включающих в себя несколько правил. Каждое такое правило описывает одно животное, Дадим описание нескольких животных:
animal_is(“тигр”) :– i
t_is(“млекопитающее”),
it_is(“хищник”),
positive(“имеет”, “рыжий цвет”),
positive(“имеет”, “черные полосы”).
animal_is("гепард") :–
it_is("млекопитающее"),
it_is("хищник"),
positive("имеет","рыжий цвет"),
positive("имеет", "черные пятна").
animal_is("зебра") :–
it_is("копытное"),
positive("имеет","черные полосы").
animal_is("пингвин") :–
it_is("птица"),
negative("умеет", "летать"),
positive("умеет", "плавать"),
positive("имеет", "черно-белый цвет").
Сходные правила должны быть для всех животных, которых предстоит классифицировать программе.
Все правила поддерживаются на следующем, более низком уровне некоторыми соподчиненными предикатами:
it_is("млекопитающее") :–
positive("имеет", "шерсть"),
positive("кормит", "детенышей молоком").
it_is("хищник") :–
positive("имеет", "острые зубы"),
positive("имеет", "когти"),
positive("имеет", "глаза, направленные вперед").
it_is("копытное") :–
it_is("млекопитающее"),
positive("имеет", "копыта"),
positive("жует", "жвачку").
Свою работу  программа начинает с использования правила
Goal animal_is(X), !,
write("Отгаданное  животное ", X),
retractall( _ ).
Далее система пытается по очереди установить истинность или ложность правил высокого уровня, т.е. найти кандидата, которого она сможет проверить на соответствие предикату animal_is.
Определение истинности такого правила влечет за собой проверку всего дерева подчиненных фактов и свидетельств, которые должны быть истинными, чтобы подтвердить основное заключение. По мере продвижения вниз по дереву программа соответственно ситуации задает нужные вопросы в нужное время для получения недостающей информации, поэтому ее поведение кажется разумным. Большая часть работы совершается правилами positive и negative, xpositive и xnegative. Они используются для проверки конкретных атрибутов животных, которые могут быть обнаружены в процессе диалога и записаны в базу данных.
Здесь задействован механизм вопросов-ответов, поэтому нам необходимо подробно рассмотреть эти правила. Ниже следует соответствующая часть программы.
database
xpositive( symbol, symbol )
xnegative( symbol, symbol )
Clauses
positive( X, Y ) :–                                    % Положительный ответ обнаружен
xpositive( X, Y ), !.                                           % в базе данных
positive( X, Y ):–
xnegative( X, Y ), !, fail.                   % Отрицательный ответ  обнаружен в базе данных
positive( X, Y ) :–                                    % Задается вопрос, для которого
ask( X, Y, yes ), !.                              % ожидается положительный ответ
ask( X, Y, yes ) :–
write( X, " оно ", Y, “?\n”),
readchar( Reply ),
ans_pos( X, Y, Reply ).
ans_pos( X, Y, 'y' ):– assertz( xpositive( X, Y )).
ans_pos( X, Y, 'n' ):– assertz( xnegative( X, Y )), !, fail.
Когда механизм вывода доходит до места, где требуется узнать, был ли установлен некоторый атрибут животного, он использует правила positive и negative. (Здесь у нас приведен предикат positive, соответствующий положительному значению атрибута. Сходный по работе с ним предикат negative записывается симметрично.)
Первая из статей предиката positive заставляет систему непосредственно просмотреть информацию, уже включенную в базу данных. Если атрибут в ней найден, процесс заканчивается. Второе правило этого предиката инициирует поиск отрицания того, что мы пытаемся установить, и если оно найдено, значение атрибута становится ложным, система переходит к проверке следующего правила animal_is. Если же фактов нет среди истинных и ложных, программа задает вопрос пользователю, при этом любой полученный ответ запоминается с целью непосредственного или последующего применения.
Все факты, что программа помещает в базу данных, всегда имеет вид пары, состоящей из глагола и свойства, например:
xpositive("имеет","перья").
Поэтому легко создать грамматически правильное предложение для предъявления его пользователю, поставив слово "оно" между глаголом и свойством. Пользователь, вероятно, введет символы "y" или "n" в ответ на запрос, а запоминающее правило занесет информацию в базу данных посредством одного из двух предикатов:
xpositive (verb, attribute)
xnegative (verb, attribute).
Можно просмотреть протокол диалога после его окончания, если сохранить содержимое динамической памяти под каким-либо именем. Команда сохранения, например, может иметь вид: save(“mybd”).

Для проведения повторной консультации с программой следует сначала очистить динамическую базу данных от ответов на вопросы, заданные при ведении последнего диалога. Они продолжают находиться в базе данных и будут влиять на следующие результаты, если их не удалить. Сделать это можно с помощью стандартных предикатов очистки динамической базы данных. Предикат retrectall( _ ) позволяет удалить все факты, т.е. полностью очистит динамическую память.

3.9.2. Программы классификации с прямой цепочкой рассуждений.

Стратегия прямого вывода состоит в том, что задается последовательность вопросов, построенных таким образом, что каждый из них позволяет отбросить большую группу потенциальных ответов, благодаря чему значительно сужается пространство поиска. Так продолжается до тех пор, пока не остается один определенный ответ. Движение начинается с корня классификационного дерева и заканчивается в концевой вершине, продвижение по дереву направляется данными, т.е. дополнительной информацией, получаемой в ходе диалога.
Животные классифицированы в различные категории, имеющие характерные черты: млекопитающие, хищники, копытные и т.д. Одна категория переходит в другую при выполнении некоторых условий. Например, категория «хищник» переходит в категорию «гепард», если выполняются условия: «животное имеет рыжий цвет", "имеет животное темные пятна».
Знания в этой системе представляют собой правила, имеющие вид:
rule( N, CAT1, CAT2, COND ).
Здесь N - порядковый номер правила,
CAT1 - выражение, стоящее в левой части правила и характеризующее признак класса (подкласса и т.д.), к которому относится данное правило;
CAT2 - содержание правила в правой части, содержащее вывод из этого правила;
COND - список номеров условий, определяющих правило.
Условие имеет вид:
cond( N, CONDTEXT ),
где  N - номер условия,
CONDTEXT - текст условия.
Таким образом,  база знаний рассматриваемой экспертной системы следующая:
rule( 1, "хищник", "гепард", [ 1, 2 ] )
rule( 2, "хищник", "тигр", [ 1, 3 ] )
rule( 3, "копытное", "жираф", [ 5, 4, 2 ] )
rule( 4, "копытное", "зебра", [ 3 ])
rule( 5, "птица", "страус", [5, 7 ] )
rule( 6, "птица", "пингвин", [ 9, 7 ] )
rule( 7, "птица", "альбатрос", [ 10 ] )
rule( 8, "животное", "млекопитающее", [ 11,12 ] )
rule( 9, "животное", "птица", [ 8, 13 ] )
rule( 10, "млекопитающее", "хищник", [ 14, 15, 16 ] )
rule( 11, "млекопитающее", "копытное", [ 17, 18 ] )
cond( 1, "оно имеет рыжий цвет" )
cond( 2, "оно имеет темные пятна" )
cond( 3,"оно имеет черные полосы" )
cond( 4, "оно имеет длинную шею" )
ond( 5, "оно имеет длинные ноги" )
cond( 6, "оно летает" )
cond( 7, "оно имеет черный и белый цвет" )
cond( 8, "оно имеет перья" )
cond( 9, "оно плавает" )
cond( 10, "оно летает хорошо" )
cond( 11, "оно имеет шерсть" )
cond( 12, "оно кормит детенышей молоком" )
cond( 13, "оно откладывает яйца" )
cond( 14, "оно ест мясо" )
cond( 15, "оно имеет когти" )
cond( 16, "оно имеет острые зубы" )
cond( 17, "оно жует жвачку" )
cond( 18, "оно имеет копыта" )
Легко видеть, что такой способ представления знаний реализует конструкцию вида ЕСЛИ-ТО:
если САТ1 отвечает условиям СOND, то САТ1 есть САТ2. С другой стороны, отношение rule очень похоже на продукционное правило, дополненное списком истинности применения продукции. Продукционное правило позволяет использовать рекурсивный механизм продвижения по дереву, что и используется в настоящей реализации.
В целом все описание соответствует древовидной структуре представления информации, в которую хорошо вписываются различные классификационные системы. Такая программа организует диалог с пользователем в процессе консультаций, модификацию базы знаний, а также имеет систему объяснений.
В режиме консультации система рассматривает пользователя как расширение программы и извлекает из него отсутствующие факты, которые необходимы для оценки цели. В результате в базу данных, в зависимости от того, выполняется данное условие или нет, присоединяются предикаты
yes(N)  или  no(N),
где N - номер условия, являющегося первым аргументом предиката cond.
Основным рабочим предикатом ЭС является рекурсивный предикат go. Этот предикат организует просмотр дерева базы знаний, выделение очередного правила и выдачу рекомендаций в случае достижения концевой вершины классификационного дерева. Он также позволяет хранить предысторию процесса консультации (т.е. набор использованных правил) для реализации системы объяснений.
go( _ , Mygoal ):-                                                           /*Цель достигнута */
not(rule( _ , Mygoal, _ , _ )),
write( "Отгаданное  животное: ",Mygoal ).
go( HISTORY, Mygoal ):-
rule( RNO, Mygoal, NY, COND ),
check( RNO, HISTORY, COND ),
go( [ RNO | HISTORY ], NY ).
Первое правило предиката  go  является базовым для рекурсии, оно соответствует достижению конечной вершины (в базе данных нет правила rule, где конечная вершина дерева стоит вторым аргументом). Если конечная вершина не достигнута, работает рекурсивное правило предиката  go. Выбирается очередное правило rule из базы данных.
Предикат  check, входящий во второе правило предиката go, производит проверку списка условий COND на достоверность, т.е. выполняет поиск уже имеющихся фактов, относящихся к данным условиям. Если ответ на эти условия имеется в базе данных в виде фактов  yes(BNO) или  no(BNO), проверка на этом заканчивается. В случае, если требуемые факты не обнаружены, определяется запрос пользователю с помощью предиката  inpq. Если проверка check заканчивается ложно, то выбирается следующее правило из базы знаний. Если же проверка успешна, номер правила присоединяется к списку успешных правил HISTORY, по которому можно восстановить историю поиска, а текущей целью становится третий аргумент правила  rule, что означает переход к следующему уровню дерева:
check( RNO, HISTORY, [ BNO | REST ] ) :-  yes( BNO ), !,          % Ответ “yes” обнаружен
check( RNO, HISTORY, REST ).                                           
check( _ , _ , [ BNO | _ ] ) :- no( BNO ), !, fail. % Ответ “no” обнаружен
check( RNO, HISTORY, [ BNO | REST ] ) :-
cond( BNO, TEXT_COND ),
inpq( HISTORY, RNO, BNO, TEXT_COND ),
check( RNO, HISTORY, REST ).
check( _ , _ , [ ] ).
Предикат inpq  запускает диалоговый механизм, посредством которого система получает недостающую информацию. Система задает пользователю вопросы, представляющие собой  условия истинности конкретного правила, при этом пользователь может ответить  “yes”, “no” или “why”.  Третий ответ означает, что пользователю нужно знать, почему система задала такой вопрос. В этом случае намерения системы демонстрируются в виде цепочки правил и целей, соединяющих эту информацию с исходным вопросом.
inpq( HISTORY, RNO, BNO, TEXT_COND ) :-
write( "Это правда, что ", TEXT_COND),
readln( ANS ),
do_answer( HISTORY, RNO, TEXT_COND, BNO, ANS ).
Предикат do_answer  организует наполнение базы данных новыми фактами, полученными в процессе диалога с пользователем, а также реализует систему объяснений, которая предоставляет пользователю набор правил, на основании которых было принято то или иное решение:
do_answer( _ , _ , _ , BNO, “yes” ) :- assert( yes( BNO )), write( yes ), !.           % Ответ “yes”
do_answer( _ , _ , _ , BNO, “no” ) :- assert( no( BNO )), write(no), !, fail.          % Ответ “no”
do_answer( HISTORY, RNO, TEXT_COND, BNO, “why” ) :- !,                                       % Ответ “why”
rule( RNO, Mygoal1, Mygoal2, _ ),
sub_cat(Mygoal1,Mygoal2,Lstr),
concat("I try to show that: ",Lstr,Lstr1),
concat(Lstr1,"\nBy using rule number ",Ls1),
str_int(Str_num,RNO),
concat(Ls1,Str_num,Ans),
show_rule(RNO,Lls1),
concat(Ans,Lls1,Ans1),
report(HISTORY,Sng),
concat(Ans1,Sng,Answ),
display(Answ),
do_answer(HISTORY,RNO,TEXT,BNO, ANS).
Вдумчивый читатель мог заметить, что программа отличается от предыдущей по своим возможностям, а именно: список условий содержит только позитивные признаки. Преодолеть этот недостаток можно, по-видимому, разными способами: либо внести отрицание на уровне строковых констант («оно не летает»), либо дополнить отношение rule еще одним аргументом – списком негативных признаков, что является более грамотным.
Такая экспертная система может быть достаточно просто преобразована в оболочку экспертной системы, достаточно базу фактов, представляющую базу знаний предметной области, вынести в динамическую память. Разделение базы данных и программы позволяет реализовать оболочку экспертной системы. Такая оболочка может быть настроена на любую предметную область, которую можно представить в виде классификационного дерева. Программа можно дополнить  модулями, присущими экспертной системе: модулем работы в режиме консультаций, блоком объяснений, обеспечить возможности просмотра, редактирования и пополнения базы знаний.
Рассмотрим еще одну задачу, реализуемую с помощью прямой цепочки рассуждений, не использующую рекурсивный механизм поиска. Прямая цепочка на каждом шаге позволяет отбрасывать примерно половину оставшихся возможностей, т.е. она используется, когда количество начальных состояний параметров невелико, а пространство состояний неуправляемо (множество перестановок, сочетаний). Это может быть в случаях, когда параметры независимы. Программа называется: «Прогнозирование наводнения».
В качестве примера возьмем ситуацию, нужно ли эвакуировать расположенный в горах небольшой городок при угрозе наводнения. Прежде всего, исходя из задачи, нужно выявить факторы, которые будут использоваться для прогноза:
1. Уровень воды в водоеме. Если уровень воды высок, то существует угроза наводнения. Уровень воды также может повышаться за счет стоков дождя и талого снега.
2. Дождь. Если ожидаются обильные дожи и уровень воды высок, то есть вероятность наводнения.
3. Температура. Если предсказана теплая погода и с гор в реку стаяло много снега, то есть опасность наводнения.
4. Снег. В расчет принимается количество снега в горах.
В качестве атрибутов этих факторов будут использоваться значения лингвистических переменных согласно нечеткой логике : высокий, низкий, мало, много, теплый и т.д.
  Отметим, что эти факторы,  в основном,  независимы и могут проявляться в различных сочетаниях. Прогноз, в зависимости от сочетания факторов, может принимать одно из трех значений: эвакуировать, усилить внимание, не беспокоиться.
Как и ранее, представим базу знаний в виде дерева решений, а затем преобразуем его в правила вида ЕСЛИ-ТО. Дерево решений представлено на рис. 3….

Рис. 3. Дерево решений для системы прогнозирования наводнений
Для каждого пути можно записать правило. Совокупность всех правил составит базу знаний.
ЕСЛИ НЕ (уровень воды высокий)  
И  НЕ (дождь обильный)
ТО прогноз = не беспокоиться
ЕСЛИ НЕ (уровень воды высокий)  
И  дождь обильный
И снегу много
И температура высокая
ТО прогноз = усилить внимание
ЕСЛИ НЕ (уровень воды высокий)  
И  дождь обильный
И снегу много
И НЕ (температура высокая)
ТО прогноз = не беспокоиться
ЕСЛИ НЕ (уровень воды высокий)  
И  дождь обильный
И НЕ (снегу много)
ТО прогноз = не беспокоиться
ЕСЛИ уровень воды высокий
И  дождь обильный
ТО прогноз = эвакуировать
ЕСЛИ уровень воды высокий  
И  НЕ (дождь обильный)
И снегу много
И температура высокая
ТО прогноз = эвакуировать
ЕСЛИ уровень воды высокий  
И  НЕ (дождь обильный)
И снегу много
И НЕ (температура высокая)
ТО прогноз = усилить внимание
ЕСЛИ уровень воды высокий  
И  НЕ (дождь обильный)
И НЕ (снегу много)
И НЕ (температура высокая)
ТО прогноз =  не беспокоиться
Преобразовать дерево решений в набор правил, как помнит читатель, можно, проследив все возможные пути, ведущие к логическому выводу.
До сих пор все было как раньше. Теперь начинается интересная реализация. Первоначально будет запущен предикат proverka, который занесет прогноз в динамическую базу данных. Извлечь его оттуда уже не представляет сложности (предикат prognoz).
start :- proverka,
prognoz( P ),
write( “Наш прогноз - ”, P ).
Предикат proverka состоит из четырех тестов, каждый из которых соответствует проверке одного из перечисленных факторов:
proverka :- test1( F1 ),               % Уровень воды
test2( F1, F2 ),                       %  Дождь
test3( F1, F2, F3 ),                 % Снег
test4( F1, F2, F3, _ ).  % Температура
proverka.
В ходе диалога переменные F1, F2, F3 могут принимать одно из двух значений: «y» или «n». Прямой вывод будет направляться этими значениями, причем ответы, полученные из предыдущего теста, будут использоваться как входные для последующих тестов. Приведем цепочки вывода:
test1( ‘y’ ) :- it_is( “уровень воды высокий” ).            % Проверка продолжится
test1( ‘n’ ).                                                                    % Проверка продолжится
test2( ‘y’, ‘y’ ) :- it_is( “дождь обильный” ),
assert( prognoz( “эвакуировать” )).                       % Конец ветви
test2( ‘y’, ‘n’ ).
test2( ‘n’, ‘y’ ) :- it_is( “дождь обильный” ).
test2( ‘n’, ‘n’ ) :- assert( prognoz( “не беспокоиться” )).
test3( ‘y’, ’n’, ‘y’ ) :- it_is( “снегу много”).
test3( ‘y’, ’n’, ‘n’ ) :- assert( prognoz( “не беспокоиться” )).
test3( ‘n’, ’y’, ‘y’ ) :- it_is( “снегу много”).
test3( ‘n’, ’y’, ‘n’ ) :- assert( prognoz( “не беспокоиться” )).
test4( ‘y’, ‘n’, ‘y’ ,’y’ ) :- it_is( “температура высокая”),
assert( prognoz( “эвакуировать” )).
test4( ‘y’, ‘n’, ‘y’ ,’n’ ) :- assert( prognoz( “усилить внимание” ).
test4( ‘n’, ‘y’, ‘y’ ,’y’ ) :- it_is( “температура высокая”),
assert( prognoz( “усилить внимание” )).
test4( ‘n’, ‘y’, ‘y’ ,’n’ ) :- assert( prognoz( “не беспокоиться” ).
It_is( X ) :- write( X, “?”),                            % Механизм диалога
readchar( A ), A = ‘y’.
Когда по какой-либо ветви достигается решение, факт прогноза помещается в динамическую базу данных.
Предикат proverka рассчитан на выполнение четырех проверок, хотя иногда достаточно двух или трех, при этом ответ помещается в базу данных. Однако предикат продолжает свою работу и пытается удовлетворить следующие тесты, что невозможно. В результате первое правило предиката proverka закончится ложно, сработает второй дизъюнкт. Ответ уже находится в динамической базе данных, и извлечь его оттуда несложно.
Отметим, что в этой реализации программы классификации ответы пользователя не сохраняются, однако при некоторой модификации несложно их запоминать и, соответственно, реализовать механизм объяснений. Кроме того, можно рассмотреть случаи, когда лингвистическая переменная принимать не только бинарные значения («снегу много» или «снегу мало»), но и любые дискретные.
Когда правила логически обусловлены, т.е. используются дискретные альтернативные данные (Да/Нет),  удается написать достаточно простую программу для получения определенных выводов. Однако возможно применять и непрерывные переменные. Если они носят вероятностный характер, то нужен определенный метод обработки этих вероятностей. Существуют различные подходы к реализации неопределенностей в задачах поиска .
Один из ранних подходов к представлению неопределенностей использовал теорию вероятностей, позже это механизм был заменен применением так называемого коэффициента определенности импликации, или уверенности (certainty factor, CF):
Если есть S то имеется D с уверенностью CF.
Значения коэффициента определенности лежат в диапазоне [ -1, +1 ].
С другой стороны, признак S тоже может проявиться с некоторой «силой», т.е. имеет свой CF. Правило комбинирования, позволяющее вычислить коэффициент определенности заключения, когда известен коэффициент определенности посылки, лежащей в его основе, записывается так:
CF (заключение) = CF(посылка) * CF(импликация)
Посылка правила может состоять из нескольких атомарных посылок, каждая из которых имеет свой коэффициент определенности. Они могут быть связаны между собой логическим операциями типа И, ИЛИ, НЕ. Принято, что коэффициент определенности посылки равен коэффициенту определенности наименее надежной из посылок:
CF( S1 И S2) = min(CF( S1 ), CF( S2)).
Коэффициент определенности дизъюнкции посылок равен коэффициенту определенности сильнейшей ее части:
CF( S1 ИЛИ S2) = max(CF( S1 ), CF( S2)).
Если сделать допущение, что события независимы друг от друга, программа может быть реализована достаточно просто. Продукционным правилам можно приписать числа, указывающие относительную важность (вес) фактов:
rule(hypothesis A, AND((cond1, CF1), (cond2, CF2), …) .

Для реализации механизма вывода на таких знаниях вполне можно использовать рекурсивный алгоритм, дополненный некоторым способом комбинирования посылок.

3.9. Обработка текстов

В разборе фраз ограниченного естественного языка особенно ярко проявляются преимущества Пролога по сравнению с традиционными процедурными языками программирования. Пролог обладает большими возможностями по сопоставлению объектов с образцом, поэтому данный язык программирования хорошо подходит для обработки текстов и разработки различного рода компиляторов.
В данном разделе продемонстрируем две системы грамматического разбора. Система грамматического разбора – это программа, которая распознает синтаксические объекты в потоке лексем, т.е. реализует какую-либо формальную грамматику. Грамматика представляет систему правил, определяющих принадлежность фразы к языку. Общеизвестны  две основные стратегии грамматического разбора: нисходящая (сверху вниз) и восходящая (снизу вверх).
Система нисходящего грамматического разбора базируется на стратегии с обратной цепочкой рассуждений, а система восходящего разбора – с прямой. Следовательно, реализация на Прологе системы нисходящего разбора может быть осуществлена достаточно прямолинейным способом.
Продемонстрируем систему разбора сверху вниз примером простейшего синтаксического анализатора предложений. В описанной системе используется грамматика, которую можно схематически представить так:
предложение --> именная_группа   глагольная_группа
именная_группа --> определение    существительное
именная_группа --> существительное
глагольная_группа --> глагол   существительное
Система нисходящего грамматического разбора начинает работу с принятия некоторой гипотезы, а затем проверяет верность следствий этой гипотезы по данным, содержащимся во входном списке. Первоначальной гипотезой может служить, например, предположение о том, что во входном списке можно обнаружить нетерминал "предложение". В соответствии с грамматическим правилом для нетерминала "предложение" данная гипотеза разбивается на две субгипотезы: на предположения о том, что во входном потоке содержатся группа подлежащего (именная группа) и группа сказуемого (глагольная группа). Эти две гипотезы в свою очередь разбиваются на субгипотезы более низкого уровня. Процесс разделения гипотез на субгипотезы продолжается до тех пор, пока система не встретит терминал (конечный символ, слово из словаря). В этом случае она пытается установить факт наличия терминала в начальной позиции входного списка.
Более важной сферой применения систем грамматического разбора  является построение так называемого дерева грамматического разбора в том или ином виде, в котором явно указаны классы объектов и существующие между ними отношения
Пример анализатора, строящего дерево синтаксического разбора для простого английского предложения: "every man that lives loves a woman". Это предложение соответствует следующей грамматике, записанной в БНФ:
<SENTENCE>     ::= <NOUN PHRASE> <VERB PHRASE>
<NOUN PHRASE> ::=<DETERMINER> <noun> <RELATIONAL CLAUSE>
<DETERMINER>  ::= < > | <determiner>
<RELATIONAL CLAUSE>  ::= < > | <relative> <VERB PHRASE>
<VERB PHRASE>  ::= <verb>  |  <verb> <NOUN PHRASE>
Здесь прописными буквами записаны нетерминальные (промежуточные) символы, строчными – терминальные (словарь), вертикальная черта обозначает альтернативы для разбора. Например, глагольная группа <VERB PHRASE>  может состоять из одного глагола <verb>  или глагола, за которым следует дополнение в форме именной группы: <verb> <NOUN PHRASE> .
Данная грамматика, в частности, разбирает приведенную выше фразу, а также более короткие варианты, в которых могут отсутствовать отдельные группы и члены предложения:
"every man loves a woman", "every man that lives loves", "man loves".
Дерево грамматического разбора нашего предложения:

Рис.1. Дерево грамматического разбора предложения
Результат грамматического разбора должен получиться в виде объекта Пролога:
SENTENCE = sent(nounp(determ(“every”), “man”, relcl(“that”, verb(“lives”))),
verbp(“loves”, nounp(determ(“a”),”woman”, none))).
Грамматика, заданная в виде БНФ, переписывается в  секции DOMAINS с учетом синтаксиса Пролога:

DOMAINS                       
DETERM   = none ; determ( STRING )
NOUNP    = nounp( DETERM, STRING, RELCL)
RELCL    = none ; relcl( STRING, VERBP )
VERBP    = verb( STRING ) ; verbp( STRING, NOUNP )
SENTENCE = sent( NOUNP, VERBP )
К области DOMAINS добавляется еще одно определение – список строковых величин. В качестве списка строк будет представлено разбираемое предложение, например список ["every”, “man’’, “loves”, “a”, “woman"]:
DOMAINS
TOKL     = STRING*
Каждая строка представляет одно слово предложения и называется лексемой (токеном).
Все предикаты, участвующие в грамматическом разборе, делятся на две группы. Предикаты с префиксом is_ относятся к словарю, находят для выделенного слова его грамматическую статью (является ли слово существительным, или глаголом или т.д.) и далее идентифицируют его по словарю.
Предикаты с префиксом  s_  выделяют соответствующую грамматическую конструкцию:  s_nounp выделяет именную группу,    s_verbp – глагольную группу и т.д.:
PREDICATES
s_verbp( TOKL, TOKL,  VERBP )
 Все предикаты с префиксом  s_  имеют три аргумента. Первым аргументом TOKL является входной список лексем (слов), третий аргумент – это название выделенной грамматической конструкции, т.е. то, что удалось выделить из входного списка на данной стадии грамматического разбора. Второй аргумент образован частью списка, оставшегося после того, как из входного списка будет взята разобранная часть предложения.
При записи клозов предикатов с префиксом  s_   должны учитываться следующие особенности:

• число клозов каждого предиката соответствует количеству их альтернатив в описании DOMAINS;
• В первую очередь записываются клозы, имеющие самую сложную реализацию.

Рассмотрим разбор глагольной группы. Поскольку в секции DOMAINS описаны две альтернативы разбора глагольной группы:
VERBP    = verb( STRING ) ; verbp( STRING, NOUNP ),
у нас в реализации предиката разбора глагольной группы должно быть два клоза s_verbp. Это следующие предложения:
s_verbp ( [ VERB | TOKL ], TOKL1, verbp( VERB, NOUNP )):–
is_verb (VERB),
s_nounp ( TOKL, TOKL1, NOUNP).
s_verbp ( [ VERB | TOKL ], TOKL, verb( VERB )):–
is_ver ( VERB ).
Первый клоз s_verbp  предполагает, что в начале списка слов находится глагол  VERB и пытается распознать его по словарю предикатом is_verb (VERB). Если распознавание успешно, из остальной части списка  TOKL выделяется именная группа NOUNP, тогда остаток списка после удачного распознавания – список TOKL1, возвращаемый третий аргумент – выделенная глагольная группа verbp(VERB, NOUNP). Второй клоз предиката s_verbp  разбирает глагольную группу, состоящую из одного глагола.
В приведенном фрагменте
Полная программа на Прологе:
DATABASE                                     % Слова , которые должны быть распознаны
det( STRING )                            % Определитель
noun( STRING )             % Существительное
rel( STRING )                             % Предлог
verb( STRING )                          % Глагол
DOMAINS               % Описание грамматики
DETERM   = none ; determ( STRING )
NOUNP    = nounp( DETERM, STRING, RELCL)
RELCL    = none ; relcl( STRING, VERBP )
SENTENCE = sent( NOUNP, VERBP )
VERBP    = verb( STRING ) ; verbp( STRING, NOUNP )
TOKL     = STRING*
PREDICATES
is_det( STRING )
is_noun( STRING )
is_rel( STRING )
is_verb( STRING )
s_determ( TOKL, TOKL, DETERM )
s_nounp( TOKL, TOKL, NOUNP )
s_relcl( TOKL, TOKL, RELCL )
s_sentence( TOKL, TOKL, SENTENCE )
s_verbp( TOKL, TOKL, VERBP )
tokl( STRING, TOKL )
tom( TOKL )
run1
run2( STRING )
sen_an
GOAL    makewindow(1,6,0,"",0,0,25,80),
sen_an.
CLAUSES
sen_an:–  write("Try: every man that lives loves a woman"),
readln( LIN ), LIN >< "" ,
tokl( LIN, TOKL ),                   % перевод строки в список токенов
s_sentence( TOKL, _ , SENT ),
write("PROLOG OBJECT=",SENT," "),
readchar( _ ), clearwindow, !.
tokl( STR, [ TOK | TOKL ] ) :–
fronttoken( STR, TOK, STR1 ),
tokl( STR1, TOKL ).
tokl( _ ,[  ] ).
s_sentence( TOKL, TOKL2, sent( NOUNP, VERBP )):–
s_nounp( TOKL, TOKL1, NOUNP),            
s_verbp( TOKL1, TOKL2, VERBP ),
TOKL2=[ ],! .               /* Признак успешного грамматического разбора – остаток списка пуст*/
s_sentence( _ , _ , _ ):–write(">> Sentence not recognized \n"), fail.
% именная группа
s_nounp( TOKL, TOKL2, nounp( DETERM, NOUN, RELCL )):–
s_determ( TOKL, [ NOUN | TOKL1 ], DETERM ),
is_noun( NOUN ),
s_relcl( TOKL1, TOKL2, RELCL ).
% Группа дополнения
s_determ( [ DETERM | TOKL ], TOKL, determ( DETERM )):–
is_det( DETERM ).
s_determ( TOKL, TOKL, none ).
% Группа дополнения
s_relcl( [ REL | TOKL ], TOKL1, relcl( REL, VERBP )):–
is_rel( REL ),
s_verbp( TOKL, TOKL1, VERBP ).
s_relcl( TOKL, TOKL, none ).
% глагольная группа
s_verbp( [ VERB | TOKL ], TOKL1, verbp( VERB, NOUNP )):–
is_verb( VERB ),
s_nounp( TOKL, TOKL1, NOUNP ).
s_verbp( [ VERB | TOKL ], TOKL, verb( VERB )):–
is_verb( VERB ).
is_noun( X ):– noun( X ), !.
is_noun( X ):– noun( Y ), concat( Y, "s", X ).
is_det( X ):– det( X ).
is_rel( X ):– rel( X ).
is_verb( X ):– verb( X ), !.
is_verb( X ):– verb( Y ), concat( Y, "s", X ), !.
is_verb( X ):– verb( Y ), concat( Y, "ed", X ), !.
is_verb( X ):– verb( Y ), concat( Y, "es", X), !.
is_verb( X ):– verb( Y ), concat( Y, "ing", X ).
% словарь
det( "every" ).
det( "a" ).
noun( "man" ).
noun( "woman" ).
rel( "that" ).
rel( "who" ).
rel( "whom" ).
rel( "which" ).
rel( "that" ).
verb( "love" ).
verb( "live" ).

Несколько сложнее реализуется на Прологе система восходящего грамматического разбора, т.к.  она базируется на прямой цепочке рассуждений. Однако такая система имеет то преимущество, что может работать с рекурсивными правилами, которые могли бы вызвать бесконечное зацикливание в системе нисходящего разбора.
Примером для реализации восходящей грамматики с рекурсивными правилами является синтаксический анализатор математических выражений. Такая система начинает работу с данными и переходит к простым синтаксическим объектам, а затем и к более сложным. В то время как система нисходящего разбора управляется в основном гипотезами, система восходящего грамматического разбора управляется данными.
В следующем примере на вход подается алгебраическое выражение в виде строки, которое может содержать имена переменных и знаки плюс и умножить. Результат работы программы – запись выражения в префиксной форме, когда знак операции предшествует операндам.
Предикат run начинает работу программы с создания окна, считывает исходное выражение в переменную  STR . Следующий предикат  tokl  переводит строковую переменную в список TOKL токенов (лексем), далее предикат  s_exp запускает рабочий предикат plusexp, с которого собственно начинается работа анализатора.
Процедура  multexp  первую лексему (имя переменной) переводит в префиксную форму и проверяет остаток на наличие после нее (лексемы) операции умножения предикатом  multexp1. Если знак "*" присутствует, последний предикат переводит сомножители в префиксную форму.
Предикат  plusexp1  проверяет остаток после знака  "+" на наличие операции умножения предикатом  multexp. Если умножения нет, слагаемые также переводятся в префиксную форму.
domains
TOKL = STRING *
EXP=var( STRING );
plus( EXP, EXP );
mult( EXP, EXP )
PREDICATES
run
tokl( STRING, TOKL )
s_exp( TOKL, TOKL, EXP )
multexp( TOKL, TOKL, EXP )
multexp1( TOKL, TOKL, EXP, EXP )
plusexp( TOKL, TOKL, EXP )
plusexp1( TOKL, TOKL, EXP, EXP )
elmexp( TOKL, TOKL, EXP )
GOAL
run.
CLAUSES
run:–  makewindow(1, 2, 7, "", 0, 0, 25, 80),
readln( STR ), tokl( STR, TOKL ),
s_exp( TOKL, _ , EXP ), write(EXP), nl.
tokl( STR, [ TOK | TOKL ] ):–
fronttoken( STR, TOK, STR1 ),
tokl( STR1, TOKL ).
tokl( _ , [  ] ).
s_exp( IL, OL, EXP ):–plusexp( IL, OL, EXP ).
plusexp( IL, OL, EXP2 ):–
multexp( IL, OL1, EXP1 ),
plusexp1( OL1, OL, EXP1, EXP2 ).
plusexp1( [ "+" | IL ], OL, EXP1, EXP3 ):–
multexp( IL, OL1, EXP2 ),
plusexp1( OL1, OL, plus( EXP1, EXP2), EXP3 ).
plusexp1( IL, IL, EXP, EXP ).
multexp( IL, OL, EXP2 ) :–
elmexp( IL, OL1, EXP1 ),
multexp1( OL1, OL, EXP1, EXP2 ).
multexp1( [ "*" | IL ], OL, EXP1, EXP3 ):–
elmexp( IL, OL1, EXP2),
multexp1( OL1, OL, mult(EXP1, EXP2), EXP3).
multexp1( IL, IL, EXP, EXP ).
elmexp( [ NAME | IL ], IL, var( NAME ) ).

Упражнения

1. Разработайте систему грамматического разбора для построения интерфейса на ограниченном естественном языке для вопросно-ответной системы. Фразы языка примерно следующие: 
Where is the white block?
On the table.
Pick up yellow block!
Is there a block at the table?
Which block supports the cube?
Small black block.
Is there anything on that block?
The box.
2. Разработайте систему грамматического разбора для перевода правил некоторой базы знаний во внутреннюю форму представления. Правило базы знаний имеет структуру:
<type> <name>
DISPLAY <display string>
<function name> <function parameters>,
где
<type> – одно из hypothesis, intermediate или data;
<name> – идентификатор правила, любое допустимое имя Пролога;
DISPLAY – ключевое слово;
<display string> – строка, заключенная в кавычки;
<function name> – имя функции, может быть одно из AND, OR, NOT, YESNO;
<function parameters> – имена других правил, которые обрабатываются функцией.
Форма внутреннего представления должна быть следующая:
rule(type_string, name_string, display_sting, function_info).
Например, для правил
hypothesis car
DISPLAY “use a car”
AND
intermediate car_speed
DISPLAY “speed car”
OR car_factor car_map
data drive_yourself
DISPLAY “Do you want to drive yourself?”
YESNO
форма внутреннего представления должны быть следующая:
rule(“hypothesis”, “car”, “use a car”, and_rule([“car_speed”, “car_dist”, “car_cost”]).
rule(“intermediate”, “car_speed”, “speed car”, or_rule([“car_factor”, “car_ map”]).
rule(“data”, “drive_yourself”, “Do you want to drive yourself?”, yesno_rule).
Указание 1. Исходные правила хранятся в файле. Для перевода файла в строку используйте стандартный предикат file_str.
Указание 2. Для выделения первой подстроки из строки используйте стандартный предикат fronttoken.

3.10. Примеры

Пример №1:

/* Copyright (c) 1986, '92 by Prolog Development Center */

trace

domains

name, sex, occupation, object, vice, substance = symbol

age=integer

predicates

person(name, age, sex, occupation)

had_affair(name, name)

killed_with(name, object)

killed(name)

killer(name)

motive(vice)

smeared_in(name, substance)

owns(name, object)

operates_identically(object, object)

owns_probably(name, object)

suspect(name)

/* * * Facts about the murder * * */

clauses

person(bert, 55, m, carpenter).

person(allan, 25, m, football_player).

person(allan, 25, m, butcher).

person(john, 25, m, pickpocket).

had_affair(barbara, john).

had_affair(barbara, bert).

had_affair(susan, john).

killed_with(susan, club).

killed(susan).

motive(money).

motive(jealousy).

motive(righteousness).

smeared_in(bert, blood).

smeared_in(susan, blood).

smeared_in(allan, mud).

smeared_in(john, chocolate).

smeared_in(barbara, chocolate).

owns(bert, wooden_leg).

owns(john, pistol).

/* * * Background knowledge * * */

operates_identically(wooden_leg, club).

operates_identically(bar, club).

operates_identically(pair_of_scissors, knife).

operates_identically(football_boot, club).

owns_probably(X, football_boot) :-

person(X, _, _, football_player).

owns_probably(X, pair_of_scissors) :-

person(X, _, _, hairdresser).

owns_probably(X, Object) :-

owns(X, Object).

/* * * * * * * * * * * * * * * * * * * * * * *

* Suspect all those who own a weapon with *

* which Susan could have been killed. *

* * * * * * * * * * * * * * * * * * * * * * */

suspect(X) :-

killed_with(susan, Weapon) ,

operates_identically(Object, Weapon) ,

owns_probably(X, Object).

/* * * * * * * * * * * * * * * * * * * * * * * * * *

* Suspect men who have had an affair with Susan. *

* * * * * * * * * * * * * * * * * * * * * * * * * */

suspect(X) :-

motive(jealousy) ,

person(X, _, m, _) ,

had_affair(susan, X).

/* * * * * * * * * * * * * * * * * * * * *

* Suspect females who have had an *

* affair with someone that Susan knew. *

* * * * * * * * * * * * * * * * * * * * */

suspect(X) :-

motive(jealousy) ,

person(X, _, f, _) ,

had_affair(X, Man) ,

had_affair(susan, Man).

/* * * * * * * * * * * * * * * * * * * * * * * * * * *

* Suspect pickpockets whose motive could be money. *

* * * * * * * * * * * * * * * * * * * * * * * * * * */

suspect(X) :-

motive(money) , person(X, _, _, pickpocket).

killer(Killer) :-

person(Killer, _, _, _) ,

killed(Killed) ,

Killed <> Killer , /* It is not a suicide */

suspect(Killer) ,

smeared_in(Killer, Goo) ,

smeared_in(Killed, Goo).

Пример №2:

/* Copyright (c) 1986, '92 by Prolog Development Center */

/* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

* Simple tree-building procedures *

* create_tree(A, B) puts A in the data field of a one-cell tree giving B *

* insert_left(A, B, C) inserts A as left subtree of B giving C *

* insert_right(A, B, C) inserts A as right subtree of B giving C *

* *

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * */

domains

treetype = tree(string, treetype, treetype) ; empty()

predicates

create_tree(string, treetype)

insert_left(treetype, treetype, treetype)

insert_right(treetype, treetype, treetype)

clauses

create_tree(A, tree(A, empty, empty)).

insert_left(X, tree(A, _, B), tree(A, X, B)).

insert_right(X, tree(A, B, _), tree(A, B, X)).

goal

/* First create some one-cell trees... */

create_tree("Charles", Ch),

create_tree("Hazel", H),

create_tree("Michael", Mi),

create_tree("Jim", J),

create_tree("Eleanor", E),

create_tree("Melody", Me),

create_tree("Cathy", Ca),

/* ...then link them up... */

insert_left(Ch, Mi, Mi2),

insert_right(H, Mi2, Mi3),

insert_left(J, Me, Me2),

insert_right(E, Me2, Me3),

insert_left(Mi3, Ca, Ca2),

insert_right(Me3, Ca2, Ca3),

/* ...and print the result. */

write(Ca3,'\n').