Принципы логического программирования
1.2. Математическая основа языка Пролог
1.2.1 Организация вычислительного процесса
1.2.2. Использование переменных
1.2.3. Синтаксис фактов и правил
1.3. Бэктрекинг
1.2. Примеры
1.2. Математическая основа языка Пролог
Программа
на Прологе
включает в
себя постанову
задачи в виде
множества
формул логики
предикатов
первого
порядка и описания
цели –
формулировку
теоремы, которую
нужно
доказать,
исходя из
множества фактов
и правил,
содержащихся
в этой постановке.
Формализм
исчисления
предикатов
первого
порядка
оказался
удобным для
описания постановки
задачи на
языке,
близком к естественному.
Таким
образом, язык
Пролог имеет
четкую математическую
основу. В
основе языка
лежит исчисление
предикатов
первого
порядка, и в
этом смысле
язык
является
подмножеством
формальной
логики. Но
Пролог
включает не все
формальное
исчисление, а
только некоторое
его
подмножество,
представленное
хорновскими
дизъюнктами.
Дадим
несколько
определений.
Пусть
имеется
некоторое множество
объектов,
называемое предметной
областью.
Выражение P(X1,
X2, …, Xn), где
Xi, i=1,…,n – так
называемые
предметные
переменные, а
P принимает
значения 0
или 1,
называется логической
функцией
или предикатом.
Предикат от n
переменных
называют n-местным.
Предикат P(X1, X2,
…, Xn)
задает
отношение
между
элементами X1,X2,…,Xn и
обозначает
высказывание,
что �X1,X2,…,Xn
находятся
между собой в
отношении P�.
Например,
если
отношение родитель(X,Y)
означает, что
X является
родителем
для Y (но не
наоборот!), то
высказывание
родитель(�царь
Петр I�,
�царевич
Алексей�)
является
истинным, а
отношение родитель(�царь
Петр I�,
�царевна
Софья�) –
ложным. Важно
понимать, что
имена
отношений и
их размерность
(�арность�)
произвольны
и зависят
только от
целей их
использования.
Из подобного
рода
элементарных
отношений с
помощью
логических
связок
образуют более
сложные
отношения,
которые в
свою очередь
являются
предикатами,
то есть могут
принимать те же
значения –
�истина� или
�ложь�. В
качестве связок
используются
конъюнкция
(логическое
И),
дизъюнкция
(логическое
ИЛИ),
импликация
(логическое
следование),
отрицание,
эквивалентность.
Рассмотрим
классический
пример
рассуждений
с
использованием
логических
связок. Пусть
имеются
следующие
рассуждения
на
естественном
языке (в
данном случае
– аксиомы):
Все люди
смертны.
Сократ –
человек.
Теорема,
логически
вытекающая
из этих двух
аксиом:
Сократ
смертен.
Эти аксиомы
можно
переписать
так (в
терминах
исчисления
предикатов):
Для всех X,
если X –
человек, то
смертен X
И человек(
Сократ )
Соответственно
наш пример
можно
перевести на
Пролог (пока
еще без учета
синтаксиса версии
PDC Prolog):
смертен( Х) :-
человек ( Х ).
человек( сократ
).
Здесь
собственное
имя �Сократ�,
представляющее
строковую
константу,
записано с
маленькой
буквы,
поскольку во
всех версиях
Пролога с
большой
буквы
записывается
имя переменной.
При работе
этой
небольшой
программы
можно задать
системе вопрос:
является ли
Сократ
смертным, и
система
ответит �Да�:
? смертен( сократ ).
Да
Это простой
пример, но
его
достаточно,
чтобы показать
целесообразность
использования
Пролога для
реализации
различного
рода рассуждений,
потому что
можно задать
большое количество
фактов и
правил,
Система,
построенная
с помощью
Пролога,
самостоятельно
проделает
тяжелую
работу,
пробираясь
по цепочке
через факты и
правила в
поисках
логического
вывода.
Существуют
отличия
синтаксиса
логики предикатов
от языка PDC Prolog.
Соответствие
можно видеть
в таблице 1.
|
|
Обозначение в логике предикатов |
Обозначение в языке PDC Prolog |
|
и |
& |
запятая |
|
или |
v |
точка с запятой или точка |
|
если |
=> |
:- |
|
не |
~ |
not |
В языке
Пролог
исчисление
предикатов
ограничено
специальными
выражениями,
называемыми хорновскими
дизъюнктами. Хорновской
дизъюнкт
имеет вид:
~P1 v ~P2 v … v ~ Pm v
Pn,
где P1, P2, … Pm, Pn
– предикаты
(термы,
логические
формулы). В данной
записи
предикатов
мы
акцентировали
внимание на внешнем
представлении
дизъюнкта в
виде структуры,
состоящей из
предикатов,
без перечисления
их возможных
аргументов.
Как мы видели
на примерах
выше,
предикат
имеет аргументы,
что, вообще
говоря, в
Прологе
необязательно.
(В
математической
логике
предикат без
аргументов
называется
высказыванием.)
В последнем
выражении
только
формула Pn
без
отрицания, и
в этом
главная
особенность хорновского
дизъюнкта.
Это
выражение
может быть
переписано в
виде:
P1 & P2 & … & Pm => Pn ,
и оно имеет
следующую
интерпретацию:
из P1 и P2 и … и Pm следует Pn.
Последнее
выражение
по-прежнему
называется
дизъюнктом,
хотя от
знаков
отрицания и дизъюнкции
перешли к
импликации и
конъюнкции.
Особенность хорновского
дизъюнкта:
справа от
знака
следования
стоит только
одно
следствие из
некоторого
множества
дизъюнктов,
записанных слева.
В синтаксисе
Пролога
последнее
выражение
записывается:
Pn :- P1, P2, … , Pm.
Важно
запомнить,
что
следствие
оказалось записанным
слева, а
поскольку
Пролог базируется
на хорновских
дизъюнктах, в
левой части
импликации
(заключения)
содержится
единственный
литерал.
Последнюю
запись
утверждения
Пролога
можно
трактовать
двумя способами:
- Декларативный смысл: Pn истинно, если одновременно истинны P1, P2, … , Pm.
- Процедурный смысл: для того, чтобы выполнить Pn, надо последовательно выполнить P1, P2, … , Pm.
Логика хорновских
дизъюнктов
эквивалентна
полной
теории предикатов
первого
порядка,
применяемой
для
доказательства
на основе
опровержения.
Механизм
логического
вывода
использует
метод
резолюций,
применяющийся
для автоматического
доказательства
теорем, который
был
предложен
Робинсоном (1965
г.) .
Процесс
поиска
доказательства
на основе метода
резолюции и
составляет
суть выполнения
программы на
Прологе.
Однако
знание этих
понятий явно
необязательно
для того,
чтобы начать
программировать
на Прологе.
Поэтому мы
сосредоточимся
на
прагматическом
аспекте программирования
на Прологе,
опуская
теоретическое
обоснование,
которое
достаточно
подробно
изложено в
литературе.
См.,
например, Адаменко
А., Кучуков
А. Логическое
программирование
и Visual Prolog в
подлиннике.
СПб.: �БВ-Петербург�,
2003. – 990 с.
1.2.1 Организация вычислительного процесса
Программа
на Прологе
включает
набор процедур,
каждая из
которых представляет
собой
определенный
предикат. Предикат
имеет общую
форму:
А :– В1,
В2, ... , Вn. ,
которая
интерпретируется : "А
является
истинным,
если В1,
В2, ..., Вn
являются
истинными".
Таким
образом,
значок “ :-
“
соответствует
обозначению
�если�. Предикат,
содержащий
условия
истинности,
является
правилом.
Когда n=0,
т.е. говорят,
что
отсутствуют
условия истинности,
то такое
предложение
выражает факт,
и это
записывается
"А." (точка
в конце
записи
предиката
обязательна).
Поскольку
факт не
содержит
условий
истинности, в
Прологе факт
всегда
является
истинным.
В данной
форме записи
часть
выражения,
стоящая
слева от
знака “ :- “,
называется
головой
дизъюнкта (в
нашем
примере "А"),
а выражение,
стоящее
после этого
значка, называется
телом
дизъюнкта,
т.е. В1, В2,
... , Вn
– это тело,
или хвост
дизъюнкта.
Пролог-программа
должна иметь
цель, поскольку
вычисление
такой
программы
всегда начинается
от цели.
Достичь цели
всегда означает,
что она
логически
следует из
правил программы.
Можно
рассматривать
программу
как запись
аксиом, а
цель –
теорему,
которую
следует
доказать.
Если получен
запрос (т.е.
цель, которую
нужно
удовлетворить),
Пролог
пытается
определить
его
истинность
двумя
способами.
Во-первых,
цель успешно
удовлетворяется
(т.е.
считается
истинной),
если она
сопоставляется
с
существующим
фактом (так
как факты
всегда
являются
истинными).
Во-вторых,
цель
считается
истинной,
если она
сопоставляется
с головой “А”
правила " А,
если В1,
... , Вn "
и если
подцели В1, ... , Вn могут
быть
завершены
успешно. В
случае
успешного
сопоставления
Пролог выдает
ответ "yes",
т.е. цель
согласована.
Термин �сопоставление�
обозначает
совпадение
цели с
головой факта
или правила и
относится к
одному из
двух базовых
механизмов
логического
вывода. Другой
базовой
операцией является
унификация.
Унификация
она
применяется
в том случае,
если
предикат
имеет
аргументы.
Если попытка
сопоставить
подцель с
фактами в
базе данных завершается
неудачей и
остаются
альтернативные
(еще не
применявшиеся
правила или
факты),
Пролог будет
осуществлять
возврат и
использовать
эти альтернативы.
Если все
альтернативы
закончились
неудачно, то
считается,
что
начальная цель
неудовлетворительна.
В этом случае
выдается
ответ "no".
1.2.2 Использование переменных
В
Пролог-программе
нет никаких
выражений,
кроме
предикатов, и
цель тоже
представляет
собой
некоторый
предикат (или
последовательность
предикатов).
В качестве
аргументов
цель может
содержать
константы
или переменные.
Переменная
представляет
собой неконкретизированную
величину,
которую
Пролог должен
конкретизировать,
т.е. найти
объекты-константы,
которые при
их
подстановке
вместо переменных
обеспечивают
достижение
цели. Неконкретизированная
переменная
считается
свободной, а
если выполнена
подстановка
константой,
то связанной.
После того,
как цель, содержащая
переменные,
будет
согласована, Пролог
выдаст
значения,
которыми
будут заменены
переменные,
входящие в
цель.
Рассмотрим
вышеприведенный
пример:
родитель(�царь
Петр I�,
�царевич
Алексей�).
Спросим эту
небольшую
программу,
чьим родителем
является царь
Петр I:
? родитель(
�царь Петр I�, X ).
Чтобы
ответить на
вопрос, нужно
вместо X подставит
константу
�царевич
Алексей�. В этом
случае
переменная X
конкретизируется
константой. В
этом примере
имела место
унификация.
Понятие
унификации
пришло из
математической
логики, где
ему
соответствует
подстановка
значений
вместо
переменных
при выводе
логической
формулы. В
Прологе
унификация
представляет
собой
универсальный
механизм
сопоставления
с образцом
для передачи
параметров . В
результате
унификации
переменная Х
получила
конкретное
значение.
Внутренние
механизмы
использования
переменных в
Прологе
весьма
различаются
от таковых в
алгоритмических
языках. В
процедурном
программировании
акцент
делается на
применение
оператора
присваивания
для
перемещения
данных из
фиксированных,
поименованных
мест их в
памяти. Эти поименованные
места
являются
переменными
программы.
Программы
символьного
языка
используют переменные,
которые
существуют
скорее виртуально
в стеке
компьютера, а
не фиксированных
местах
памяти.
Управление
данными осуществляется
посредством
сравнения с образцом,
и в
результате
этого
сравнения переменная
может
получить
конкретное
значение
(конкретизироваться),
пока
работает предикат.
Если
переменная
получила
свое значение,
то все
вхождения
такой
переменной в
некоторый
предикат
получают
одно и то
же значение и
уже не могут переконкретизироваться
Можно
сказать, что
все
переменные в
Прологе
локальные.
Переменная
может переконкретизироваться
только при
возврате к
поиску
других решений
(бэктрекинге).
Поскольку
программы
искусственного
интеллекта
предполагают
такой
возврат, переменная
может
многократно переконкретизироваться
с целью
вычисления
всех наборов
значений аргументов.
Немного о
присваивании.
Читатель уже
понял, что
один из способов
придать
значение
переменной –
передать ее
как параметр
(аргумент)
предиката. Другой
способ похож
на
классическое
присваивание,
поскольку
использует
знак равенства.
Но все-таки
следует
помнить, что
в Прологе нет
оператора
присваивания,
а есть похожий
на него
предикат
логического
сравнения, обозначаемый
знаком
равенства.
Поэтому понятно,
что
сопоставление
вида N = N + 1
бессмысленно:
величина
никогда не
может быть
равной самой
себе,
увеличенной
на единицу.
Надо использовать
другую
переменную: N1= N +
1, но зато
можно
записать: N + 1 = N1.
Рассмотрим,
как
выполняется
сопоставление
в последнем
случае. Пусть
N
конкретизировано
числом 3, N1 –
числом 4. В
этом случае
сопоставление
закончится
�истинно�.
Если N
конкретизировано
тем же
числом, а N1 не
конкретизировано,
то в
результате
сопоставления
N1 получит
значение 4, и
предикат
тоже
завершится �истинно�.
Несложно
сообразить,
какие конкретизации
переменных
дадут ложное
сопоставление.
Отметим
также, что
поскольку в
Прологе отсутствуют
глобальные
переменные,
одни и те же
имена
переменных
можно
употреблять
во многих
правилах
программы,
при этом между
такими
переменными
будет
отсутствовать
какая-либо
связь.
1.2.3 Синтаксис фактов и правил
Для того,
чтобы начать
писать
Пролог-программу,
следует
определиться,
какие
отношения
(предикаты) в
ней будут.
Имена
предикатов
выбираем
согласно
смыслу
программы. В
синтаксисе Пролога
предикат
имеет следующий
вид:
functor(d1,d2,...)
:– cond1, cond2,... .
Здесь functor
– имя
предиката;
functor(d1,d2,...)
– голова
дизъюнкта;
d1, d2,... – аргументы
предиката;
cond1, cond2,... –
условия
истинности
дизъюнкта (в
свою очередь,
предикаты),
где запятые
обозначают
связку “ И
”;
":–" - обозначение
"ЕСЛИ".
Важно
понимать, что
имена
предикатов и
их размерность
(�арность�)
произвольны
и зависят
только от
целей их
использования.
Рассмотрим
конкретное
предложение:
P :- Q, R.
где P, Q, R
– некоторые
предикаты.
Для выяснения
истинности P
следует
сначала
выяснить
истинность Q,
затем
истинность R.
Таким
образом,
запятая
между целями
обозначает
конъюнкцию
целей. Однако
в Прологе возможна
и дизъюнкция
целей: должна
быть истинной
по крайней
мере, одна из
целей.
Дизъюнкция
обозначается
точкой с
запятой:
P :- Q; R.
Смысл такого
предложения
тот же, что и
смысл
следующей
пары
предложений:
P :- Q.
P :- R.
Таким
образом,
логическая
функция �ИЛИ�
может быть
записана
двумя
способами.
Для
обозначения
логических
связок можно также
использовать
более
привычные: if, and,
or, но в
этом случае
запись
программы
получится
длиннее.
Если опущены
условия, то functor(d1,d2,...)
описывает
факт.
В качестве
первого
примера
рассмотрим
следующую
задачу.
Опишем мир
увлечений
некоторого
круга лиц.Следующим
утверждениям
на
английском
языке:
Ellen likes reading.
John likes football.
Tom likes baseball.
Eric likes reading.
Mark likes tennis.
соответствуют факты Пролога:
likes( ellen, reading ).
likes( john, football ).
likes( tom, baseball ).
likes( eric, reading ).
likes( mark, tennis ).
Имена людей записали строчными буквами, чтобы отличить их от имен переменных,
которые в Прологе начинаются с прописной буквы. Разумеется,
как будет видно далее,
в Прологе есть
возможность
записывать
имена как они
того
заслуживают. Некоторое множество фактов,
задающих объекты и отношения между ними,
уже образует простую программу на Прологе.
Таким образом,
вопрос: "Что любит Джон?" сводится к поиску объекта X, который отношение likes (нравится)
связывает с Джоном; этот объект и будет служить ответом на запрос:
? likes( john,
X ).
X = football.
(В языке PDC Prolog вместо знака вопроса,
обозначающего цель, записывается ключевое слово Goal).
Отметим, что при определении отношения между объектами существенен порядок, в котором эти объекты входят в отношение:
likes( john, football ) отличается от likes( football, john ).
Факты – важная часть программы искусственного интеллекта,
без них нельзя достичь цели.
Можно сказать, что каждая цель опирается на свои факты.
После записи фактов обычно следуют правила.
Правило всегда выражает некоторый общий закон.
Попробуем добавить один такой закон:
�Всякий Х, любящий читать – умный�. Его запись в виде правила:
clever ( X ) :- likes ( X, reading ).
Если значением факта всегда является �истина�,
то правило содержит условие истинности,
записанное в его правой части. Если задаться
целью найти всех умных людей среди имеющихся фактов, введем запрос:
? clever (X).
Система найдет два решения:
X=ellen
X= eric
Правило Пролога можно представить как небольшую процедуру с локальными переменными.
Основное отличие такой процедуры от процедуры,
написанной на процедурном языке:
предикат может выполнять несколько функций,
в зависимости от состояния аргументов
(конкретизированы они или нет).
Одно и то же отношение может быть использовано несколькими способами:
если его аргументы известны, то проверяется выполнимость отношения на этих аргументах;
если же некоторые аргументы неизвестны.
То вычисляется множество наборов значений этих переменных,
которые удовлетворяют отношению.
Например,
если имеется предикат
square (�площадь�),
связывающий длину и высоту геометрической фигуры с третьим значением (например,
площадью прямоугольника):
square( A, B, S ),
то вовсе необязательно этот предикат всегда будет вычислять только площадь S:
? square( 5, 4, S ),
Можно задавать и другие цели:
? square( X, 4, S ),
? square( X, Y, 20 ).
Разумеется,
должны быть запрограммированы все альтернативы вычислений,
т.е. при этом каждому такому состоянию аргументов соответствует своя статья предиката.
1.3. Бэктрекинг
Система
Пролог
обладает
встроенным
механизмом
логического
вывода
(перебора),
благодаря
чему от
пользователя
требуется
только
описание
своей задачи
с помощью
аппарата
логики
предикатов
первого
порядка, а поиск
решения
система берет
на себя. При
этом Пролог –
строго последовательный
язык.
Процедуры
выполняются в
нем строго по
очереди, в
том порядке,
в котором они
записаны.
Если вызов
процедуры завершен
успешно,
Пролог
продвигается
вперед, чтобы
попытаться
выполнить
следующую процедуру.
При этом в
стеке
запоминаются
все возможные
разветвления.
Если вызов
неудачен,
происходит
отход назад к
ближайшему
из предыдущих
вызовов
процедуры с
целью найти
другое
решение, при
этом
отменяются
результаты
всех
подстановок,
сделанных
после последнего
разветвления.
Такой же
возврат
осуществляется
и после
завершения
успешного вычисления
– для
получения
других
ответов. При
поиске новых
решений
теряются
решения, сгенерированные
на
предыдущих
шагах.
Рассмотрим
простую
программу на
Прологе в
виде предикатов
без
аргументов:
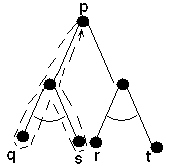 p :– q,
s.
p :– q,
s.
p :– r, t.
Эту
программу
можно
прочитать
следующим образом.
При
выполнении
процедуры p
выполняются
процедуры q и s.
Если они
завершаются
успешно, то и
процедура p
считается
успешно
завершенной.
Если это не
так, то выполняются
процедуры r и t. В этом
случае
процедура
успешно
завершается,
если r
и t завершены
успешно. В
противном
случае
процедура p
терпит
неудачу. Этот
процесс
возврата к поиску
других
решений
называется бэктрекингом
(backtracking).
Такой
алгоритм
работы можно
представить
в виде И-ИЛИ-дерева.
В прологе
применяется
стратегия
поиска в глубину,
т.е. обход
дерева
сверху вниз
слева
направо. Если
при обходе
вершины ИЛИ
какой-либо
потомок
разрешается
успешно, то
обработка
остальных
дочерних
вершин
приостанавливается,
и считается,
что вершина
ИЛИ разрешается
успешно. Если
какой-либо из
потомков И–вершины
терпит
неудачу, то
обработка
остальных ее потомков
полностью
прекращается
и данная
вершина
терпит
неудачу.
Приостановка
обработки ИЛИ-вершины
означает, что
впоследствии
возможно
повторное
обращение к
этой вершине
для поиска
других решений
(бэктрекинг).
Основными
механизмами
поиска
решения задачи
в Прологе
является
сопоставление
и унификация,
что
позволяет
решать
широкий класс
задач
наиболее
простым
способом:
путем перебора
всех
возможных
состояний.
Сначала
находится
предикат,
который
сопоставляется
с целью, а
затем
выполняется
унификация
аргументов
предиката. Унификация
– это процесс
подстановок
переменных с
целью
приведения в
соответствие
двух выражений
исчисления
предикатов.
Таким
образом,
унификация
аналогична
передаче
параметров
процедуры в
алгоритмическом
языке и в
некотором
смысле
соответствует
присваиванию.
Однако в ряде
случаев
требуется
управлять
этим
процессом и
реализовывать
другие стратегии
вывода,
встраивая их
в режим
естественного
обратного
вывода
Пролога.
Несмотря на
то, что в Прологе
отсутствуют
традиционные
управляющие
конструкции
типа
оператора
перехода,
условного
оператора,
оператора
цикла, язык
логического
программирования
позволяет
создавать
такие
механизмы
своими
методами.
Реализация
разветвляющегося
процесса осуществляется
довольно
просто:
каждой ветви
вычислений
соответствует
отдельная статья
предиката.
Пролог также
прекрасно приспособлен
для
организации
циклов. Основные
механизмы
реализации
процесса
повторений –
использование
рекурсии и
механизма бэктрекинга.
Примеры
возможных
способов
реализации алгоритмов
рассмотрены
ниже.
1.4. Примеры
�Пример №1:
/* Copyright
(c) 1986, '92 by
predicates
�� likes(symbol,symbol)
clauses
�� likes(ellen, tennis).
�� likes(john,
football).
�� likes(tom,
baseball).
�� likes(eric, swimming).
�� likes(mark,
tennis).
�� likes(bill,
Activity):- likes(tom, Activity).