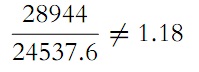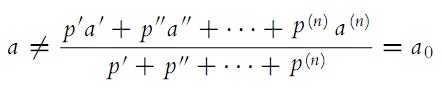
Main article.
Based on such equations and the law of large numbers, we suggest that
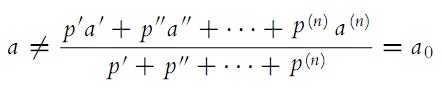
and

Only the theorem of the weight of the end result, which is expressed by the well-
known equation (22), is disregarded: the weight of the result is the same as the sum of
the weights of all parts.
In the given case, each of our 200 numbers represents the sum of nearly independent
quantities; however, the sums themselves are connected in groups of five so that only
forty of them can be regarded as independent. We have 40 groups of 500 letters each;
in no group of 100 are there letters that are adjacent in the text and this is the reason for the observed independence of the parts; on the other hand, in each group the letters of
the first hundred are next to those of the second hundred, those of the second hundred
are next to both those of the first and those of the third, etc., and for this reason, as
mentioned above, our numbers are connected in groups of five.
Under these conditions and according to the given explanations, the number

can be considered as the approximate value of the mathematical expectation of the square of the deviations of our 200 new numbers
from their mathematical expectation, which is approximately
If we pass over from the letters (samples) in hundreds to the single letters, we ascertain that the number
does not differ significantly from
the dispersion coefficient is