Диаметр Enron и смежные вопросы

В случае ориентированных графов расстояние ${\displaystyle d(u,v)}$ между двумя вершинами ${\displaystyle u}$ и ${\displaystyle v}$ определяется как длина кратчайшего пути из ${\displaystyle u}$ в ${\displaystyle v}$, состоящего из дуг. В отличие от случая неориентированных графов ${\displaystyle d(u,v)}$ может не совпадать с ${\displaystyle d(v,u)}$ и даже может случиться, что одно расстояние существует, а другое — нет. см. https://ru.wikipedia.org/wiki/Расстояние_(теория_графов)

Эксцентриситет вершины графа – расстояние до максимально удаленной от нее вершины ${\displaystyle \epsilon (v)=\max _{u\in V}d(v,u)}$. Для графа, у которого не определен вес его ребер, расстояние определяется в виде числа ребер

Радиус графа – минимальный эксцентриситет вершин ${\displaystyle r=\min _{v\in V}\epsilon (v)}$

Диаметр графа – максимальный эксцентриситет вершин ${\displaystyle d=\max _{v\in V}\epsilon (v)}$

Центр графа образуют вершины, у которых эксцентриситет равен радиусу ${\displaystyle \epsilon (v)=r}$. Центр графа может состоять из одной, нескольких или всех вершин графа

# подключим необходимые модули
import numpy as np
import networkx as nx
import scipy as sp
import timeit as ti
from scipy import stats as st

# Выделим наибольшую компоненту
# методы Networkx https://testfixsphinx.readthedocs.io/en/latest/reference/algorithms.component.html
GG=nx.read_edgelist("email-Enron.txt")
GG1 = GG.subgraph(max(nx.connected_component_subgraphs(GG), key=len))
print(nx.info(GG))
print(nx.info(GG1))

Name: 
Type: Graph
Number of nodes: 36692
Number of edges: 183831
Average degree:  10.0202
Name: 
Type: SubGraph
Number of nodes: 33696
Number of edges: 180811
Average degree:  10.7319

Расшифровка статистики SNAP

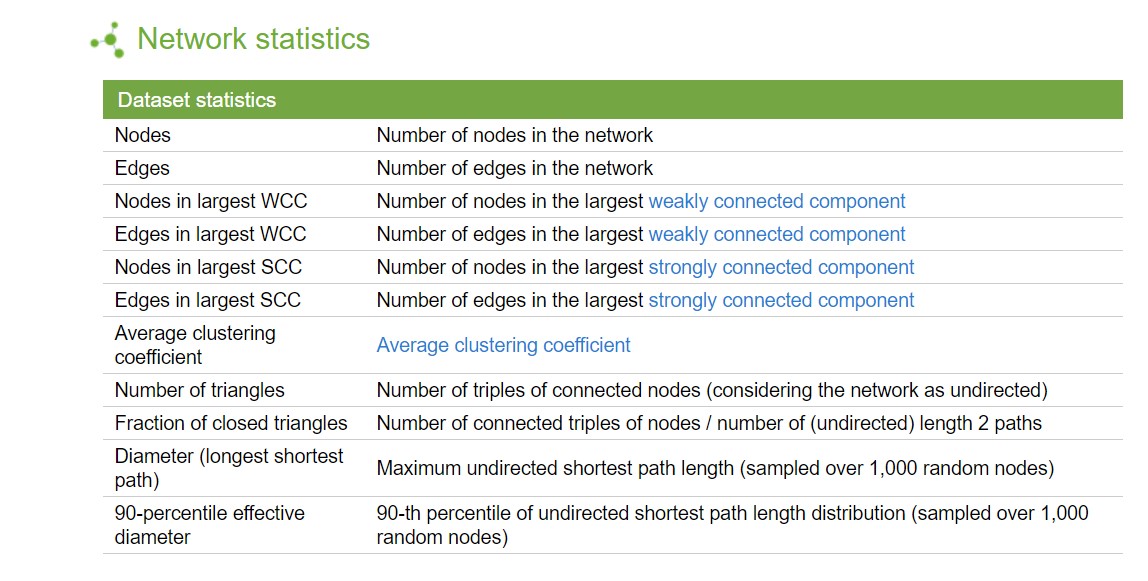
# Выберем в графе GG1 n=1000 вершин случайным образом
n=1000
sample_numbers=list(np.random.randint(0, len(GG1), n)) # список индексов 
node_list=list(nx.nodes(GG1))                          # полный список вершин

# вычислим максимальный эксцентриситет (диаметр) по n вершинам
# засечем время
t0 = ti.default_timer()                      

# для каждой вершины с индексом из списка sample_numbers 
# вычислим эксцентриситет и запишем в список eccentric
eccentric=[nx.eccentricity(GG1, node_list[x]) for x in sample_numbers]
GG1_diameter=np.max(eccentric)

delta_t = ti.default_timer()-t0
print("Diameter = ", GG1_diameter)
print("Time = ", delta_t)

Diameter =  11
Time =  1095.1492643407057

Результаты вычислений для разных n

Сравните со статистикой http://snap.stanford.edu/data/email-Enron.html

n=10 Diameter = 11 Time = 16.407611227828056

n=100 Diameter = 11 Time = 162.45421052092632

n=1000 Diameter = 11 Time = 1095.1492643407057

# Построим доверительный интервал (ДИ) для матожидания

# ДИ для среднего диаметра
def confIntMean(a, conf=0.95):
  mean, sem, m = np.mean(a), st.sem(a), st.t.ppf((1+conf)/2., len(a)-1)
  return mean - m*sem, mean + m*sem

# диаметр по n вершинам
def GG1_diameter(n):
    sample_numbers=list(np.random.randint(0, len(GG1), n)) # список индексов 
    eccentric=[nx.eccentricity(GG1, node_list[x]) for x in sample_numbers] # список эксцентриситетов
    return np.max(eccentric) 

GG=nx.read_edgelist("email-Enron.txt")
GG1 = GG.subgraph(max(nx.connected_component_subgraphs(GG), key=len))
node_list=list(nx.nodes(GG1))

n=50 # число вершин в одном прогоне
m=50 # объем выборки для построения ДИ
t0 = ti.default_timer()  
sample_GG1_diameter=[GG1_diameter(n) for x in range(m)]
delta_t = ti.default_timer()-t0

print(sample_GG1_diameter)
print("Mean = ", np.mean(sample_GG1_diameter))
print("Max = ", np.max(sample_GG1_diameter))
print("Time = ", delta_t)

[10, 11, 11, 10, 10, 10, 10, 10, 11, 11, 10, 11, 10, 11, 10, 11, 11, 11, 11, 10, 11, 11, 11, 11, 10, 11, 12, 11, 11, 11, 10, 10, 11, 10, 10, 10, 11, 10, 11, 11, 11, 11, 10, 12, 10, 10, 13, 10, 11, 11]
Mean =  10.66
Max =  13
Time =  2525.9228295874814

# ДИ для вероятностей 0.95% и 0.99%
print("2sigma", confIntMean(sample_GG1_diameter))
print("3sigma", confIntMean(sample_GG1_diameter, conf=0.99))

# С использованием встроенных функций модуля scipy.stats
mean=np.mean(sample_GG1_diameter)
sem=st.sem(sample_GG1_diameter)
max=np.max(sample_GG1_diameter)

print(st.t.interval(0.95, len(sample_GG1_diameter)-1, loc=mean, scale=sem))
print(st.t.interval(0.99, len(sample_GG1_diameter)-1, loc=mean, scale=sem))

2sigma (10.472977474387802, 10.847022525612198)
3sigma (10.410588393991944, 10.909411606008057)
(10.472977474387802, 10.847022525612198)
(10.410588393991944, 10.909411606008057)

!! тем не менее существуют вершины с эксцентриситетом > 11

nx.eccentricity(GG1, node_list[2204])

12

nx.eccentricity(GG1, node_list[22476])

12

nx.eccentricity(GG1, node_list[27344])

12