Спецификация требований

Описание

Данный проект представляет собой разработку web-интерфейса для демонстрации и тестирования системы полигональной аппроксимации.
Задача полигональной аппроксимации впервые была поставлена в картографии. В настоящее время она стала актуальной в целом ряде областей информатики, иногда слабо связанных друг c другом. Результаты проекта должны быть интегрированы с прототипом, реализующим оригинальный алгоритм полигональной аппроксимации, разработанный ранее.

Первичный список требований заказчика (пользовательские требования)

Предметная область

Пусть на плоскости определено множество прямых полос, одинаковой ширины s, произвольной длины и расположенных произвольным образом внутри некоторой площади так, что с любой точки одной полосы можно достичь любую точку другой (см. рис.). Пусть некоторый объект непрерывно движется по произвольной траектории, находясь тем не менее всегда внутри одной из полос. Будем считать, что через некоторые промежутки времени нам сообщаются координаты объекта в некоторой фиксированной системе координат. Необходимо по этим данным восстановить ломаную, описывающую движение объекта по полосам. Вершины ломаной - точки перехода объекта с одной полосы на другую.

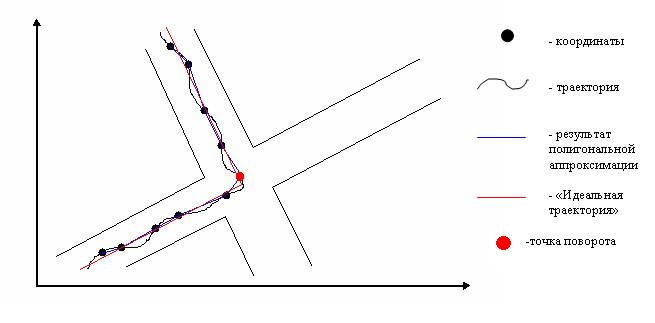
Важнейшие требуемые функции разрабатываемой системы (функциональность и ограничения)

Программное обеспечение должно обеспечивать web - интерфейс для демонстрации и тестирования алгоритма, разрешающего задачу полигональной аппроксимации и интегрировано с одной из ранее разработанных реализаций данного алгоритма (C или Jаva). А также в проекте будут реализованы следующие функции:

Генерация случайных траектории движения объекта по набору отрезков истинной траектории.
Представление на экране обозревателя в системе координат, изображённой на графическом поле, траектории движения объекта, ломаной - результата полигональной аппроксимации и "идеальной траектории"
Демонстрация и тестирование в интерактивном режиме. Здесь пользователь определяет новую точку траектории движения, а система определяет произошёл ли переход на новую полосу
Вычисление разности между "идеальной траекторией" и результатами полигональной аппроксимации по мерам максимума разности расстояния и максимума разности по одной из координат
Ведение архива тестовых примеров и результатов тестирования.

Высокоуровневая архитектура:

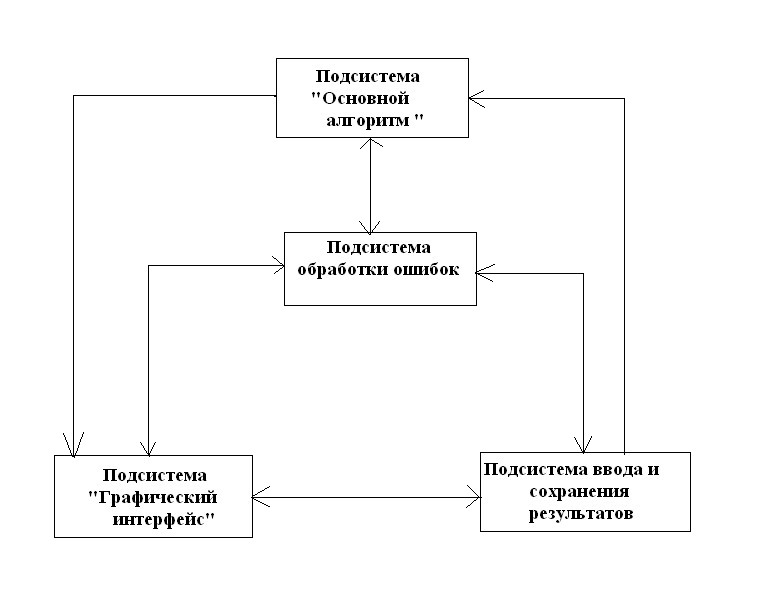
Требования к основным подсистемам:

1. Подсистема обработки ошибок

     - проверка на корректность входных данных
     - запуск основных подсистем
     - проверка работы основных подсистем

2. Подсистема "Основной алгоритм"

- осуществляет поиск точек поворота

3. Подсистема "Графическая реализация"

- отражает результаты работы алгоритма в системе координат (x,t), где t-время

4. Подсистема ввода и сохранения результатов

     - чтение входных данных из файла
     дополнительное требование: возможность ввода координат по щелчку мыши на экране
     - сохранение результатов

Модели требований (анализ и детализация)

Модель предметной области. Объекты и взаимосвязи между ними. Рамки разрабатываемой системы.

Итак, проект заключается в том, чтобы реализовать Web-интерфейс алгоритма полигональной аппроксимации. Постановка, рассматриваемая в проекте актуальна для решения задач производительности сетей технологии Wi-Fi. Задача полигональной аппроксимации заключается в том, чтобы среди множества координат определить вершины ломаной – точки перехода из одной полосы в другую.

Работа системы происходит следующим образом:

Пользователь вводит координаты, которые предаются основному алгоритму. Далее на основе результатов работы алгоритма строится траектория. Координаты вводятся из файла. Дополнительным (не обязательным) требованием к разрабатываемой системе является возможность задавать координаты щелчком мышки. Также должна быть предусмотрена возможность сохранять траектории и координаты.

Работу системы можно представить в виде следующей схемы:

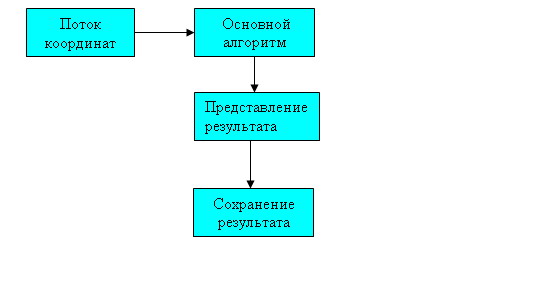
Схема, представленная ниже, показывает объекты, и связи между ними, используемые в разрабатываемой программной системе:

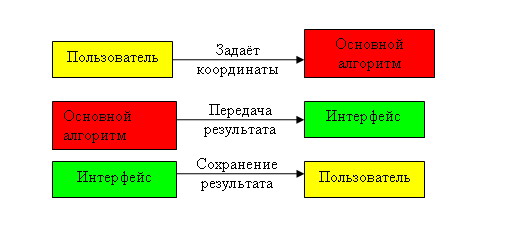
Модель пользователя системы:

Пользователь должен обладать некоторыми базовыми познаниями в предметной области, а именно должен быть знаком с основными определениями. Пользователь также должен обладать основными навыками работы на ПК (в частности пользователю необходимо уметь работать с web-браузером).

Функциональная модель:

Опишем сценарий использования системы:

В начале работы системы пользователь вводит координаты, причём координаты могут быть загружены из файла или заданы при помощи мыши, при этом осуществляется проверка корректности введённых данных (в случае загрузки данных из файла). Далее пользователю предоставляется возможность непосредственно запустить алгоритм полигональной аппроксимации. По окончании работы алгоритма пользователь имеет возможность просматривать результат – траекторию движения объекта в системе координат, изображённой на графическом поле. После этого пользователь имеет возможность интерактивно тестировать алгоритм, определяя новую точку траектории движения (данная функция является дополнительной). Пользователь также имеет возможность определить разности между "идеальной траекторией" и результатами полигональной аппроксимации по мерам максимума разности расстояния и максимума разности по одной из координат (данная функция является дополнительной). Система предоставляет пользователю возможность вести архив тестовых примеров и результатов тестирования.

Критерии аттестации

Набор базовых высокоуровневых тестов и характеристик

Данные тесты будут проверяться при аттестации ПО и удостоверяют его соответствие требованиям заказчика.

Будет проверяться работоспособность всех функций разрабатываемой системой:

Тест№1: Проверяется работоспособность функции, отвечающей за построение траектории движения объекта после выполнения алгоритма полигональной аппроксимации.
Тест№2: Проверка работоспособности функции, отвечающей за интерактивное тестирование системы, то есть проверяется, как реагирует система на добавление новой точки.
Тест№3: Проверка работоспособности функции, отвечающей за определение разности между "идеальной траекторией" и результатами полигональной аппроксимации по мерам максимума разности расстояния и максимума разности по одной из координат.
Тест№4: Проверка работоспособности функции, отвечающей за ведение архива тестовых примеров и результатов тестирования.
Тест№5: Проверка функции, отвечающей за отслеживание ошибок при загрузке координат из файла.

Глоссарий

     Аппроксимация (от лат. approximo - приближаюсь) - замена одних математических объектов (например, чисел или функций) другими, более простыми и в том или ином смысле близкими к исходным (например, кривых линий близкими к ним ломаными).
     Декартова система координат (2-х мерный случай) - 2 взаимно перпендикулярные прямые, на которых задаются единичные вектора. Данная система устанавливает взаимно однозначное соответствие между множеством точек плоскости и множеством упорядоченных пар действительных чисел.
     Точка поворота - точка, после которой движение происходит в другом направление.
     Web-интерфейс - графическое отображение данных в сети.